Tijdens het zoeken naar enkele specifieke temperaturen en materiaaleigenschappen, viel me plots op dat sommige Wikipediapagina’s niet alleen temperaturen in Celsius, Fahrenheit en Kelvin uitdrukken maar ook een lijn voorzien voor Rankine. Misschien heb jij al van Rankinegraden gehoord, maar wij in elk geval niet, en nu waren we wel benieuwd. Tijd voor een beetje research dus. In deze blogpost leggen we uit wat er zoal boven water kwam.
Wat is temperatuur?
We hebben allemaal wel een zeker begrip dat een laag getal op de thermometer wil zeggen dat je beter een extra trui aantrekt, maar wat is temperatuur nu eigenlijk? En zijn temperatuur en warmte niet stiekem hetzelfde?
Warmte is geen vloeistof, zoals de Fransman Lavoisier dacht in 1789, maar wel een gevolg van beweging, zoals Thompson acht jaar later beweerde. Dat ervaar je in het dagelijkse leven bijvoorbeeld als je in je handen wrijft. Nog eens 60 jaar later zette de Duitse fysicus Clausius de puntjes op de i door te stellen dat temperatuur in feite niets anders is dan de bewegingsenergie van de atomen of moleculen. Wat we in het alledaagse leven een warm glas water noemen, is eigenlijk gewoon een glas water waar de watermoleculen sneller bewegen dan in een koud glas water.
Over het verschil tussen warmte en temperatuur wordt al eens moeilijk gedaan. Chemici en fysici maken een onderscheid tussen beide afhankelijk van de situatie die ze beschrijven. Een stof op zich heeft een zekere temperatuur, die zoals gezegd uitdrukt met hoeveel energie erin wordt bewogen. Van warmte daarentegen wordt eigenlijk pas gesproken wanneer er interactie tussen koudere en warmere stoffen aan de gang is. Warmte is in die context een vorm van energie, zoals ook kinetische energie, lichtenergie, … die kan worden overgedragen tussen stoffen. Gelukkig hoeven wij ons daar in deze blog niet van aan te trekken gezien we het eigenlijk enkel over temperatuur zullen hebben.
Temperatuur meten in de 18e eeuw
Temperatuur meten doe je wellicht af en toe wel eens. Misschien doe je dat nog met een oude kwikthermometer, of een recentere vloeistofthermometer met een niet zo giftig mengsel van tin, gallium en indium, maar het kan evengoed met bijvoorbeeld een elektrische sensor of infraroodsensor. Gezien de veelheid aan temperatuurafhankelijke processen zijn er wel wat opties. Voor alledaags gebruik zal het resultaat vandaag de dag echter hetzelfde zijn: een getal uitgedrukt in graden Celsius (°C). Dat was echter lang niet altijd het geval. Zeker doorheen de 18e en 19e eeuw waren er heel wat verschillende temperatuurschalen in omloop, de ene al wat zinvoller dan de andere. Hieronder brengen we een bloemlezing.
We willen alvast opmerken dat er heel veel onvolledige en tegenstrijdige informatie te vinden is, onder meer doordat deze schalen vaak na hun initiële definitie verfijnd werden en doordat de conversie naar moderne eenheden niet altijd even makkelijk te ontcijferen valt. Wij deden onze uiterste best om niet bij te dragen aan deze misinformatie door aan de hand van meerdere bronnen te werken en te toetsen aan wetenschappelijke kennis. Toch kan er altijd een foutje ingeslopen zijn, dus als je dit verhaal als bron zou gebruiken, lees dan kritisch en laat het ons gerust weten als je een fout opmerkt.
Celsius/centigrade (~1742)
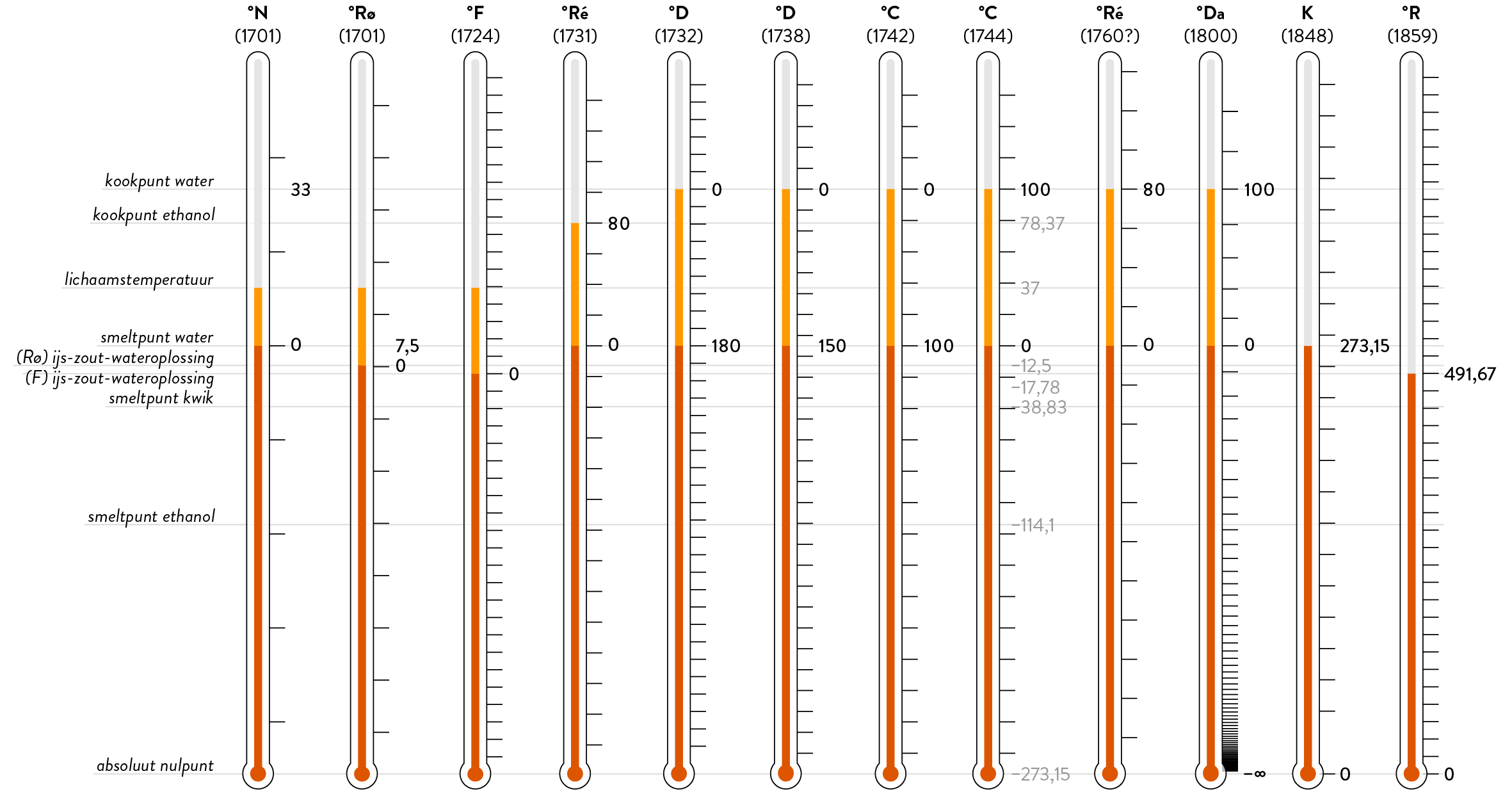
Onze gebruikelijke schaal in graden Celsius bestaat al sinds 1742, al was dat toen onder de naam centigrade. De Zweed Anders Celsius had deze schaal niet uit de lucht geplukt, maar was nauwkeurig naar het gedrag van water gaan kijken. Eerst stelde hij vast dat water zich heel stabiel gedraagt, mits de luchtdruk gelijk is: kokend water in Uppsala is bijvoorbeeld net zo warm als in Berlijn, en een emmer ijswater is net zo koud als een glas ijswater (1).
Daarna deelde hij de mogelijke temperaturen tussen het smelt- en kookpunt van water netjes op in 100 graden. Het woord graad betekent immers niet meer dan een “deel van een schaalverdeling”. Deze honderddelige schaal kon ook voor warmere of koudere stoffen gebruikt worden door vanuit deze twee punten eenvoudigweg een gelijkmatige verdeling op een kwikthermometer aan te duiden.
Celsius was trouwens niet diegene die de thermometer uitvond. De (niet zo accurate) galileithermometer bestond al meer dan honderd jaar. Zelfs de nauwkeurigere thermometers met glazen buisjes gevuld met alcohol (wijn) door Ole Christensen Rømer en de kwikthermometer van Daniel Fahrenheit bestonden al aan het begin van de 18e eeuw. Beide mannen stelden daarbij natuurlijk ook hun eigen schaal voor.
Rømer (~1701)
Die schalen leunden nog sterk aan bij de toentijds gebruikelijke werkwijze waarbij de koudste winterdag en warmste zomerdag werden aangegeven om de gebruiker een relatieve indicatie van de temperatuur te geven. Rømer stelde (min of meer gelijktijdig met Newton) voor het eerst een gekalibreerde schaal voor, een met vaste punten en een aantal gelijk verdeelde lijntjes tussenin. Die schaal begon bij 0°Rø voor een oplossing van zout, ijs en water en plaatste het kookpunt van water op zo’n 60°Rø. De precieze motiveringen lijken tussen de verschillende versies en verbeteringen van zijn schaal verloren gegaan. Zo nam hij later ijswater —zoals ook Celsius zou gaan doen — als betrouwbaarder referentiepunt voor 7,5°Rø. Gezien de gebruiken in die tijd is het echter aannemelijk dat hij zijn schaal wilde starten met iets kouder dan het smeltpunt van ijs, opdat zulke temperaturen doorheen de winter dan niet met negatieve getallen zouden moeten worden aangeduid.
Fahrenheit (~1724)
Fahrenheit bouwde op deze schaal verder. Eerst ging hij daartoe over naar een kwikthermometer — kwik zet namelijk gelijkmatiger uit bij het opwarmen dan wijn. Daarna startte hij eveneens met een specifieke zoutoplossing om 0°F vast te leggen. Hij besloot bovendien om vooral een schaal te creëren waar voor praktisch gebruik geen breuken nodig zouden zijn. Na wat foefelen vermenigvuldigde hij uiteindelijk de schaal van Rømer ongeveer met 4, zodat hij landde bij zo’n 96°F voor de menselijke lichaamstemperatuur en een derde daarvan, 32°F, voor het smeltpunt van water. Naarmate de tijd vorderde, is deze schaal ook herwerkt geraakt naar een beter reproduceerbare schaal van 32°F (smeltpunt water) tot 212°F (kookpunt water).
Delisle (~1732)
Het verkrijgen van simpele getallen voor alledaags gebruik was niet alleen een bezorgdheid van Fahrenheit. Ook Celsius verkoos initieel een indeling waarbij 0°C het kookpunt van water was en 100°C het smeltpunt van ijs, net omgekeerd dus. Negatieve getallen vermijden stond schijnbaar ook op het to-dolijstje van Joseph-Nicolas Delisle want ook hij plaatste het kookpunt van water bij 0°D en nam positieve getallen voor koudere temperaturen. Vanuit 0°D mat hij hoeveel een volume kwik krimpt bij lagere temperaturen in honderdduizendsten. Dit deed hij voor meer dan 2000 stappen tot hij zelfs de koudste dagen in Sint-Petersburg kon opmeten. Josias Weitbrecht heeft deze schaal een vijftal jaar later zo herwerkt dat 150°D het smeltpunt van ijs zou zijn. De Delisleschaal werd in die vorm tot in de 19e eeuw gebruikt in Rusland.
Réaumur(~1731)
Ook dichter bij huis ging een andere Fransman, René-Antoine de Réaumur, met een thermometer aan de slag, in zijn geval een alcoholthermometer. Hij begon zijn schaal eveneens aan 0°Ré bij het smeltpunt van water, maar gezien het kookpunt van alcohol lager ligt dan dat van water nam hij het kookpunt van alcohol als tweede referentiepunt. Hij stelde dat die temperatuur 80°Ré bedroeg. Deze waarde ligt — wellicht toevallig — vrij dicht bij het gekende kookpunt van ethanol (78,37 °C).
Enige verwarring onstond in latere jaren omdat andere wetenschappers het idee van een 80-delige schaal overnamen naar hun nieuwe (kwik)thermometers die wel hogere temperaturen aankonden. Het werd namelijk al snel de gewoonte om ook voor de bovengrens water te gaan gebruiken. De Réaumurschaal, die initieel zowat gelijkliep met de Celsiusschaal, wordt daardoor in huidige bronnen beschreven als een schaal die een factor 4/5 afwijkt.
Newton (~1701)
Toen ook Isaac Newton een temperatuurschaal wou opstellen, sloeg hij een heel andere weg in dan zijn tijdsgenoot Rømer. Hij besloot met een blikje lijnzaadolie aan de slag te gaan in plaats van met wijn gevulde glazen tubes. Ook hij startte braafjes met 0°N voor het smeltpunt van ijs. Voor het tweede referentiepunt landde ook Newton op de menselijke lichaamstemperatuur, na experimenteren met allerhande andere waarden zoals koude buitenlucht of gloeiende kolen.
Hij besloot dit 12°N te noemen, wellicht omdat dit getal vele delers heeft, en omdat Newton voornamelijk geïnteresseerd was in erg warme zaken zoals de smeltpunten van metalen. Later merkte hij op dat water onder die assumpties rond 33°N kookt. Achteraf gezien kunnen we vaststellen dat deze temperatuurschaal erg lijkt op de Celsiusschaal: de twee schalen verschillen slechts een factor 3.
Wedgewood(~1783)
Ook Josiah Wedgewood had een bijzondere substantie waarvan hij het uitzetten en inkrimpen mat: klei. Hij had hier echter wel een praktische reden toe. Als pottenbakker wilde hij graag weten hoe warm de kleioven was, maar kwik kookt al bij 356°C en dat maakt glazen kwikthermometers onbruikbaar bij hogere temperaturen. Hij plaatste dus kleien staven in zijn ovens, vergezeld van een schaalmarkering. Waar klei rood begint te gloeien (zo’n 580°C) tekende hij 0°W op en vervolgens breidde hij zijn schaal uit tot 240°W. Een zo’n Wedgewoodgraad werd in eerste instantie als zo’n 54°C geïnterpreteerd, maar dat bleek een grove overschatting. Die schaal speelde in op een concrete nood en werd dan ook werkelijk gebruikt door vele pottenbakkers … maar het bleek al gauw dat die bij lange na niet accuraat was. Zodra een vijftigtal jaar later de eerste accurate pyrometers (voorlopers van de infraroodsensor) uitgevonden werden, raakte de Wedgewoodschaal dan ook in onbruik.
Dalton (~1800?)
Standaardisering was heel wat moeilijker in een tijd waar internationale communicatie dikwijls over weken en maanden moest gebeuren. Het mag dan ook niet verbazen dat heel wat wetenschappers en wetenschapskringen hun eigen schaal gebruikten. Een collectie van wel 73 historische temperatuurschalen met hun conversieformules (voor zover die nauwkeurig te bepalen vallen) vind je op deze unieke website.
Een uitzonderlijke schaal die de auteur daar aanhaalt, is die van John Dalton. In tegenstelling tot elk van de andere temperatuurschalen is deze niet lineair maar logaritmisch van aard. Handig wanneer je met erg hoge en uiteenlopende temperaturen wil werken zoals bijvoorbeeld de temperatuur van verschillende sterren, maar behalve een smeltpunt van water bij 0 en een kookpunt bij 100 is er weinig herkenbaars aan deze schaal.
In elk geval, met wat historisch getouwtrek zijn veel van deze schalen in de vergetelheid geraakt, maar twee kampen blijven bestaan. Waar de meeste mensen vandaag de Celsiusschaal gebruiken, blijft de VS team Fahrenheit.
Absoluut nulpunt en de Kelvinschaal
Op een ijzige winterdag heb je je misschien al wel eens afgevraagd, hoeveel kouder het nog kan worden. Wetenschappers hebben die vraag ook al wel eens bekeken, en hebben daar een erg precies antwoord op. Herinner je je dat temperatuur eigenlijk de aanwezige hoeveelheid bewegingsenergie is? Logischerwijze is de koudst mogelijke temperatuur dan deze waar er géén beweging meer is. Met behulp van gekende wetmatigheden zoals de gaswetten kan men bepalen dat die temperatuur –273,15°C bedraagt. Merk op dat deze temperatuur zuiver theoretisch is — hoewel er heel wat onderzoek gebeurt naar materiaaleigenschappen bij ultralage temperaturen, is het absolute nulpunt in praktijk onbereikbaar en gebeurt dat onderzoek steeds een kleine fractie van een graad erboven.
Dit werd in 1848 het nulpunt voor een nieuwe schaal, dit keer door William Thomson (beter gekend als Lord Kelvin) die zijn stapgrootte simpelweg overnam van de Celsiusschaal. Behalve een leuke theoretische denkoefening blijkt een dergelijke absolute schaal ook erg nuttig voor berekeningen in de thermodynamica, waardoor de Kelvin de standaard werd voor wetenschappelijk gebruik. Waarom je favoriete weerman of -vrouw niet snel zal aankondigen dat het morgen 290K zal zijn, spreekt echter ook voor zich: zo’n grote getallen zijn voor dagelijks gebruik niet erg handig.
De Rankineschaal
Elf jaar later kwam de schotse fysicus Macquorn Rankine tot eenzelfde vaststelling in zijn werk rond thermodynamica. Een absolute schaal voor temperatuur zou een stuk handiger zijn dan steeds met correctietermen te moeten werken. In plaats van de schaal van zijn collega Kelvin over te nemen, besloot hij echter een gelijklopende schaal te definiëren met de stapgrootte van de Fahrenheitschaal.
Nu vraag je je ongetwijfeld af, waarom gebruikte Rankine niet gewoon de Kelvinschaal? Gezien de korte opeenvolging kun je misschien vermoeden dat de beide heren niet van elkaar afwisten, maar dat lijkt wel erg onwaarschijnlijk gezien ze beiden werkten aan de Universiteit van Glasgow. Bovendien werkten ze beide in hetzelfde vakgebied — thermodynamica — én werkten ze geregeld verder op elkaars werk — bijvoorbeeld met betrekking tot de heat death paradox.
Was de Rankineschaal dan beter of nuttiger dan de Kelvinschaal? Niet echt, op een factor 5/9 na zijn ze namelijk identiek. Het enige voordeel van de Rankineschaal was dat er makkelijker te converteren valt tussen Fahrenheit en Rankine dan tussen Fahrenheit en Kelvin. Echter, hoewel Groot-Brittannië in die tijd nog de Fahrenheitschaal gebruikte in het dagelijkse leven, was dat in wetenschappelijke contexten niet noodzakelijk het geval meer.
Volgens ons kan er dus niet veel meer achter zitten dan een persoonlijke vete of het willen sieren van het eigen ego. Wiskundige en wetenschapshistoricus Clifford Truesdell lijkt deze mening te delen. Hij schreef namelijk een heel boek getiteld “The Tragicomical History of Thermodynamics” (2) waar zowel Kelvin als Rankine uitgebreid aan bod komen.
Wordt Rankine nog gebruikt?
Wie gebruikt Rankine nog nu alle wetenschap gebruiktmaakt van SI-eenheden zoals meter, Celsius/Kelvin, gram? Wel … NASA en heel wat andere spelers in de Amerikaanse ruimtevaartsector, bleek recent nog maar eens. Na een recente poging tot lanceren van de eerste Artemisraket bleek in een persconferentie namelijk dat de poging onder meer werd uitgesteld omdat de motoren niet tot hun vereiste temperatuur van zo’n 500°R gekoeld raakten. Dat had natuurlijk heel wat verwarring onder jongere ruimtevaartenthousiasten en de nodige grappen op Twitter tot gevolg.
Na het verliezen van de Mars Climate Orbiter door het gebruik van incompatibele eenheden, zou je denken dat ze bij NASA hun lesje wel geleerd hebben. Op papier werkt NASA ook al sinds 1990 met metrische eenheden, maar gezien Artemis gebruik maakt van een SLS-raket blijkt dit in de praktijk niet het geval. Het Space Launch System is namelijk de opvolger voor het Space Shuttleprogramma dat — om politieke redenen — zo veel mogelijk originele componenten en designs hergebruikt. Gezien voor de eerste vier vluchten zelfs fysiek oude motoren van onder het stof gehaald werden, is het dus niet geheel onverwacht dat het SLS-programma nog heel wat achterhaalde empirische eenheden gebruikt. Hout vasthouden dat ze dit keer wel al hun conversies driedubbel gecontroleerd hebben dan maar?
Waarom geen graden Kelvin?
Je zag in deze blogpost al heel wat graden passeren: 0°C, 0°F, 0°R en meer, maar dan wel 0K. Dat laatste is geen tikfout, maar een echte conventie. Vaak wordt geargumenteerd dat Kelvin zonder graden genoteerd wordt omdat Kelvin in tegenstelling tot Celsius en Fahrenheit een absolute schaal is en geen schaalverdeling tussen twee vaste punten. Dit klinkt best geloofwaardig, tot je dus leert dat ook Rankine een absolute eenheid is en meestal wél met een gradensymbool genoteerd wordt. Sommigen beweren dat ook 0R zonder gradensymbool geschreven moet worden net om die reden.
Laten we eerlijk zijn, zoals veel vreemde notaties is dit gewoon historisch zo gegroeid. Vroeger werd er zelfs ‘graden Kelvin’ gezegd, tot in 1968 besloten werd dat Kelvin net zoals gram of meter een absolute eenheid was en geen gradennotatie meer zou krijgen. Dit werd echter beslist op een conferentie omtrent metrische eenheden en dus bleef de Rankine de gradennotatie grotendeels behouden.
Negatieve absolute temperaturen
Over absolute temperaturen gesproken, eerder legden we je uit dat het absolute nulpunt, 0K, de koudst mogelijke temperatuur is. Je kan je dus wel inbeelden dat een terloopse vermelding dat er ook negatieve absolute temperaturen — soort van — bestaan, alarmbellen doet afgaan. Als je benieuwd bent waar deze ongelukkige terminologie vandaan komt, dan kun je eens gaan bladeren in deze handige FAQ van een onderzoeksgroep uit München die zich met allerhande kwantumfenomenen bezighoudt. Wij zullen dit onderwerp echter toch even links laten liggen, want ons petje gaat het wat te boven.
Mag het voor jou ook wat luchtiger zijn? Kijk dan gerust eens tussen onze vorige wetenschapsweetjes.
- Anders Celsius, “Observationer om twänne beständiga grader på en thermometer” (Observaties over twee stabiele graden op een thermometer), Kungliga Svenska Vetenskapsakademiens Handlingar (Proceedings of the Royal Swedish Academy of Sciences), vol. 3, p. 171–180, 1742. (↩)
- Clifford Truesdell, The Tragicomical History of Thermodynamics 1822–1854. Springer-Verlag, 1980. (↩)
