Grafentheorie is een algemeen framework dat toelaat om heel wat praktische problemen te modelleren en wiskundig te benaderen, waarbij het gaat over “verbindingen” — in welke vorm dan ook. Routes uitstippelen op een wegennet is een voor de hand liggend voorbeeld, maar denk bijvoorbeeld ook aan sociale netwerken, ontwerp van elektronische circuits, contact tracing tijdens pandemieën, foutgevoeligheid in computernetwerken, of zelfs draaiingen met een Rubik’s cube. Al deze voorbeelden kunnen we abstract voorstellen in de vorm van een graaf.
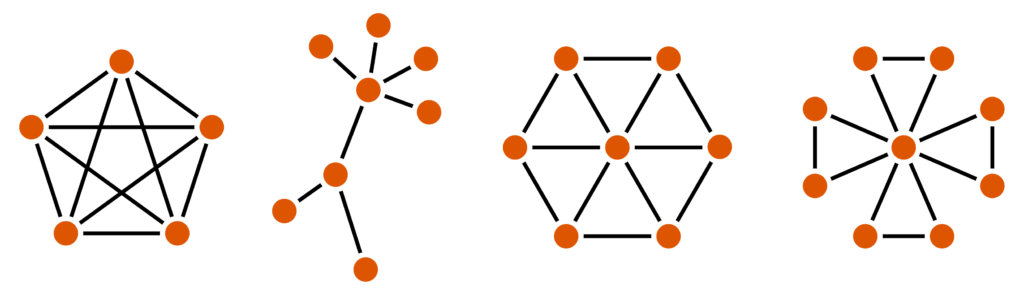
Een (enkelvoudige) graaf bestaat uit twee soorten objecten: enerzijds zijn er toppen, en anderzijds bogen die telkens twee toppen met elkaar verbinden. In de voorbeelden hieronder worden de toppen in oranje weergegeven en de bogen in zwart.
Afhankelijk van de situatie kunnen toppen en bogen van alles voorstellen, zoals steden of kruispunten verbonden door wegen, accounts op een sociaal netwerk verbonden indien ze elkaar kennen of volgen, componenten in een elektronisch circuit waartussen bedradingen moeten worden gesoldeerd, computers of servers waartussen bestanden worden uitgewisseld, posities van een Rubik’s cube die worden verbonden als ze slechts één draaibeweging verschillen, …
Soms spreekt men ook van knopen in plaats van toppen en van kanten of zijden in plaats van bogen. Daarnaast zijn er, afhankelijk van de context, tal van variaties nuttig. In een wegennetwerk bijvoorbeeld bestaan er ook eenrichtingswegen en is het nuttig om bij te houden hoe lang elke weg is. Er zijn dan gerichte grafen waarin de bogen worden voorzien van een richting, gewogen grafen waarbij de bogen een zeker gewicht dragen, gelabelde (of gekleurde) grafen waarbij de toppen of bogen een label (of kleur) toegekend krijgen, multigrafen waarbij er meerdere bogen tussen twee toppen kunnen lopen en pseudografen die bovendien lussen kunnen bevatten, … En dan zijn er nog mengelingen daarvan! Voor al deze varianten bestaan er ook geschikte variaties van de definities die volgen, maar we gaan ons hier focussen op de enkelvoudige grafen.
Twee toppen die worden verbonden door een boog, noemen we buren. Het aantal buren van een top noemen we zijn graad. In het eerste voorbeeld hierboven heeft elke top dus graad 4; in het laatste voorbeeld heeft de centrale top graad 8 en de rest graad 2. In een sociaal netwerk zijn de toppen met hoge graad bijvoorbeeld celebrity’s met veel volgers.
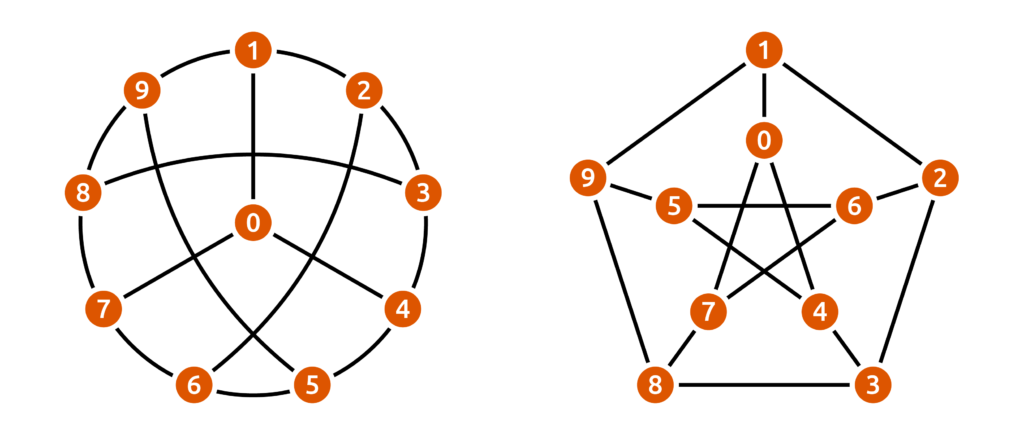
Het is van groot belang te beseffen dat een graaf op (heel veel) verschillende manieren kan worden voorgesteld, maar dat alleen de onderlinge verbanden tussen de toppen, bepaald door de bogen, van belang zijn. Hieronder staan twee illustraties die er volledig verschillend uitzien, maar wel degelijk dezelfde graaf voorstellen! De labels in de toppen helpen dit inzien: in beide illustraties heeft iedere top precies dezelfde buren.
De graaf in kwestie heet trouwens de Petersengraaf en is een van de meest iconische voorbeelden in de grafentheorie. Elke top heeft er graad 3, en de twee weergaven tonen aan dat de graaf zowel een drievoudige als een vijfvoudige symmetrie bezit.
Een pad doorheen een graaf is een sequentie van verschillende toppen doorheen de graaf, in elke stap naar een buur, en de lengte ervan is het aantal gezette stappen. In de Petersengraaf hierboven vormen de toppen gelabeld 1 – 2 – 6 – 5 – 9 – 8 – 7 een pad van lengte 6. Heel gelijkaardig is een cykel een “gesloten pad” dat weer bij de starttop uitkomt (en om randgevallen uit te sluiten, minstens lengte 3 heeft). Zo is bijvoorbeeld 1 – 2 – 3 – 8 – 9 – 1 een cykel van lengte 5. Een fietstocht langs een knooppuntenroute is een mooi voorbeeld van een cykel in een graaf, en als je een pad volgt in een sociaal netwerk, dan kom je onderweg vrienden van vrienden van vrienden … tegen.
Paden geven een natuurlijke manier om een notie van afstand in een graaf vast te leggen: de afstand tussen twee toppen is de lengte van het kortste pad dat die twee toppen verbindt. Zo liggen in de Petersengraaf elke twee toppen op hoogstens afstand 2 van elkaar. Merk op dat zo’n afstand enkel steek houdt in een graaf waarbij er überhaupt altijd zo’n paden bestaan voor elke twee toppen en die niet in losse componenten uiteenvalt — zo’n graaf wordt samenhangend genoemd.
Nog even terugkijkend naar de graaf van vriendschappen op ’s werelds grootste sociale netwerk … hoeveel vrienden zijn twee willekeurige personen gemiddeld van elkaar verwijderd? Met andere woorden, wat is de gemiddelde afstand tussen twee toppen in de graaf? Misschien heb je wel al eens gehoord van de “six degrees of separation”. Welnu, Facebook heeft in 2011 data vrijgegeven waaruit bleek dat de gemiddelde afstand toen slechts 4,74 bedroeg. Of anders gezegd, twee willekeurige personen over heel de wereld kennen elkaar (gemiddeld gezien) via slechts drie of vier tussenliggende vrienden!
Er bestaan letterlijk honderden families van grafen die op zichzelf bestudeerd worden, met kleurrijke namen zoals cactusgrafen, windmolengrafen, tandwielgrafen, kreeftgrafen, lollygrafen, pannenkoekgrafen, … Op deze blog zullen we nog heel wat puzzels uit de doeken doen en onderweg komen we een heel aantal interessante families grafen tegen. Wordt vervolgd!