Team Bollebus wenst al onze volgers een voorspoedig nieuwjaar! En omdat er wel het een en ander te vertellen valt over het getal 2025, grijpen we de gelegenheid graag aan voor enkele boeiende wiskundeweetjes. Om te beginnen is 2025 een kwadraatgetal: \[2025 = 45^2.\]
En ook die 45 is niet zomaar het eerste het beste getal, want het is een driehoeksgetal: \[45 = 1+2+3+4+5+6+7+8+9.\]
Driehoeksgetallen
Waarom een getal van die vorm een driehoeksgetal heet, wordt snel duidelijk op een figuurtje. Je kan de termen tekenen als de rijen in een driehoekig schema. De figuur hieronder bestaat in totaal uit 45 blokjes, opgedeeld in rijen van 1, van 2, van 3, … en van 9 blokjes.

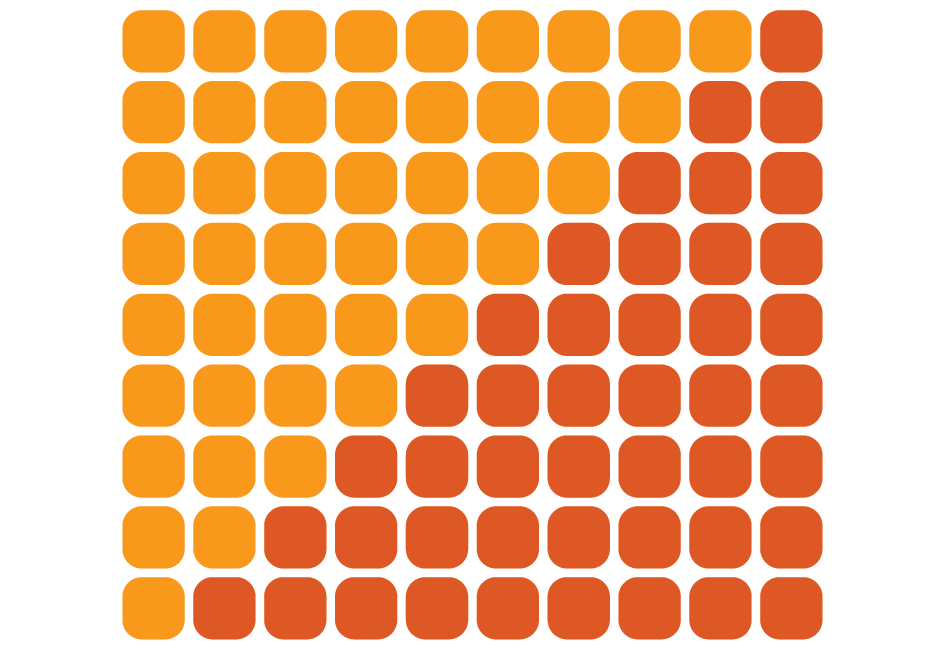
De som van de eerste negen getallen valt nu nog makkelijk rechtstreeks te tellen. Maar als men je vraagt om de eerste 100 getallen op te tellen, dus het 100e driehoeksgetal te berekenen, hoe pak je dat (slim) aan? Er is een beroemd verhaal dat Carl Friedrich Gauss, samen met Leonhard Euler een van de meest legendarische wiskundigen ooit, in de lagere school werd gevraagd om juist die grote som te berekenen. De leerkracht hoopte om alle leerlingen aan het werk te zetten en te kunnen genieten van een halfuurtje rust. Gauss zou een ogenblik later al het juiste antwoord — 5050 — gevonden hebben. Niet door dat afstompende rekenwerk bliksemsnel in zijn hoofd uit te voeren, maar wel in te zien dat er in de som een patroon zit die tot een snelle oplossing leidt. Het valt te betwijfelen of de anekdote over Gauss heel waarheidsgetrouw is (1) maar los daarvan gaat het inzicht sowieso al terug naar de oude Grieken.
Het driehoekige schema hierboven stelde de som van 1 tot en met 9 visueel voor. Door een kopie te maken van die driehoek en die ondersteboven ernaast te zetten, kun je een perfect rechthoekig schema van 9 bij 10 vakjes herkennen. En daar is het aantal vakjes makkelijk te berekenen: dat is gewoon een product! Dus het aantal blokjes in de originele driehoek was juist de helft van 9 keer 10, oftewel 45. In een algemene formule: \[1+2+\cdots+n = \frac{1}{2}\cdot n\cdot (n+1).\]
Het was via die methode dat Gauss in een-twee-drie de juiste som kon berekenen: \(\frac{1}{2}\cdot 100\cdot 101 = 5050\).
Datzelfde idee kun je ook puur in getallen uitdrukken, zonder meetkundige figuur, door de rij van getallen op te delen in goedgekozen paren met gelijke som. Zo is immers \(1+100 = 2+99 = 3+98 = 4+97 = \cdots = 50+51 = 101\). De totale som is dus inderdaad \(50 \cdot 101 = 5050\).
Kwadraten van driehoeksgetallen
Maar daarmee is nog niet alles over driehoeksgetallen gezegd, en al zeker niet over hun kwadraten. Die verschuilen namelijk een bijzonder mooie eigenschap. Niet alleen is 2025 het kwadraat van de som van de eerste negen getallen, maar ook de som van de derdemachten van die eerste negen getallen: \[(1+2+3+4+5+6+7+8+9)^2 = 2025 = 1^3 + 2^3 + 3^3 + 4^3 + 5^3 + 6^3 + 7^3 + 8^3 + 9^3.\]
Dezelfde eigenschap geldt voor alle driehoeksgetallen: \[(1+2+\cdots+n)^2 = 1^3 + 2^3 + \cdots + n^3.\]
Deze charmante identiteit wordt wel eens de stelling van Nicomachus genoemd, naar de Griek die daarvan een variant opmerkte in zijn Introductio Arithmeticae. In dat werk geeft Nicomachus vooral veel voorbeelden, zonder bewijzen (en er staan dan ook her en der flagrante onwaarheden in). Het duurde echter niet lang voor het verband tussen kwadraten en derdemachten ook rigoureus bewezen werd, niet alleen met zuiver rekenwerk maar ook met sprekende meetkundige illustraties.
Beschouw bij wijze van voorbeeld het driehoeksgetal \(1+2+3+4+5=15\). Hieronder herken je een totaal van \(15^2=225\) blokjes, geordend in een vierkant en voorzien van kleuren om de termen duidelijk te maken. We trachten nu om de blokjes te herschikken tot kubussen.

Het ene blokje helemaal links is al een kubusje. De volgende donkere band (overeenkomend met de term 3) kun je opdelen in drie vierkanten van 3 bij 3, die dus mooi gestapeld kunnen worden in een kubus van 3 bij 3 bij 3 — zie de figuur hieronder. Zo ook de volgende donkere band (overeenkomend met de term 5): daarin kun je vijf vierkanten van 5 bij 5 stapelen naar een kubus van 5 bij 5 bij 5.
De lichter gekleurde banden (overeenkomend met de even termen) vergen een lichtjes andere aanpak: als je de band op dezelfde manier in vierkanten tracht te knippen, dan blijft aan de beide uiteinden nog een half vierkant over. Voor de rest blijft het systeem behouden: er komen twee vierkanten van 2 bij 2 en vier vierkanten van 4 bij 4, opnieuw goed voor twee perfecte kubussen.

Alles samen zijn de \((1+2+3+4+5)^2\) blokjes dus te herschikken tot vijf kubussen van \(1^3 + 2^3 + 3^3 + 4^3 + 5^3\) blokjes groot. Natuurlijk vergt het een beetje argumenteren om zomaar te mogen veralgemenen naar grotere driehoeksgetallen, om zeker te zijn dat het opdelen van banden in vierkanten altijd juist uitkomt, maar wees gerust: het patroon zet zich wel degelijk verder. Prachtig toch!
- Brian Hayes, Gauss’s day of reckoning. American Scientist, vol. 94, no. 3, 2006. (↩)



Heel mooi gevisualiseerd !