Opmerking: deze blogpost is een vervolg op de post over Dobble — meer specifiek, over de meetkunde die achter dat gekende spel schuilt — en bouwt dan ook verder op enkele begrippen zonder die opnieuw in te voeren.
In de vorige blogpost werd duidelijk dat de kaarten en symbolen van het gekende spel Dobble te interpreteren vallen als punten en rechten in een meetkundige structuur (een projectief vlak). De eigenschap dat elke twee Dobblekaarten steeds één symbool gemeenschappelijk hebben, komt in die meetkundige wereld overeen met de eigenschap dat elke twee punten steeds op één rechte liggen. We lichtten er ook een tipje van de sluier over een verwant nieuw spel, dat we leerden kennen op de spellenbeurs Spiel 2023 in Essen: Møbee.
In deze blogpost gaan we dieper in op dat nieuwe spel! Net als bij Dobble schuilt er namelijk opnieuw een rijke meetkundige wereld achter. Het spel werd ontworpen en uitgegeven door prof. János Ruff van de Universiteit van Pécs, Hongarije, die onderzoek doet naar discrete wiskunde en eindige meetkunde. Samen met een enthousiast team kwam János Møbee presenteren in de prototypehal van Spiel 2023, waar hij even al enthousiast over de achterliggende wiskunde uitwijdde, over de huidige researchtopics, over de collega’s van de Universiteit Gent en andere kennissen …


Buiten het thuisland Hongarije kun je Møbee alleen nog maar terugvinden op onze webshop. Alvorens in de wiskunde te vliegen, nemen we best even een kijkje naar hoe het spel juist werkt.
Møbee: de spelregels
Het doosje van Møbee komt met enkele pakjes kaarten (met een groene, gele of rode rand). Het groene deck bestaat bijvoorbeeld uit 8 kaarten met daarop telkens 7 symbolen; het gele en rode deck bevatten wat meer kaarten die ook meer symbolen afbeelden. Niet alleen qua kaarten maar ook qua spelregels zijn er enkele varianten, maar het komt er telkens op neer dat er drie kaarten (uit hetzelfde deck) worden omgedraaid en de spelers zo snel mogelijk het ene symbool moeten vinden dat op die drie kaarten staat. Het spel is zó gemaakt dat elke combinatie van drie kaarten juist één symbool gemeenschappelijk heeft. Wie dat symbool het snelst vindt, krijgt een punt, en er worden nieuwe kaarten omgedraaid.
Spelmechanisch is Møbee duidelijk niet zo verschillend van Dobble. Tijdens het spelen voelt het natuurlijk wel uitdagender aan om meer dan twee kaarten ineens te moeten vergelijken, zeker op de rode kaarten: daar zijn er 17 van, met zo maar eventjes 20 symbolen op elk. Je bent er best even zoet mee!

Møbee: de constructie
Net als Dobble is het verre van evident om een stapel kaarten met de Møbee-eigenschap uit te stippelen zonder een gerichte methode. En ook achter Møbee schuilt er erg boeiende wiskunde met een meetkundige tintje. Opnieuw kunnen we de Møbeekaarten interpreteren als punten in een zekere meetkundige structuur. Bij Dobble ging het vervolgens over rechten die telkens twee punten verbinden en die zo correspondeerden met de gemeenschappelijke symbolen. Drie kaarten (of punten) kunnen echter ook al in een “driehoek” liggen, dus voelt het onnatuurlijk om die in “rechten” te bundelen. In deze algemenere context spreken we over blokdesigns, bestaande uit punten ingedeeld in blokken. Die blokken spelen een gelijkaardige rol als de rechten in Dobble en zullen corresponderen met de symbolen.
Blokdesigns (1) zijn een vrij breed en rekbaar begrip, maar het voornaamste criterium is dat de blokken voldoende symmetrie en spreiding vertonen over de punten. Hoeveel en welke precies, varieert doorheen de literatuur. De theorie is ontstaan uit de statistische onderzoeksplanning (design of experiments) met als doel om efficiënt en toch betrouwbaar meerdere factoren tegelijk te kunnen testen over meerdere proeven heen.
De affiene en projectieve vlakken bij Dobble zijn voorbeelden van blokdesigns (met de rechten als blokken). Voor Møbee vertaalt de cruciale Møbee-eigenschap — elke drie kaarten bevatten precies één gemeenschappelijk symbool — zich in een concreet kenmerk waaraan de gewenste blokdesigns moeten voldoen — elke drie punten liggen in precies één blok.
Net als bij Dobble bestaan er saaie constructies van zo’n blokdesign. Zo zou je aan elke combinatie van drie verschillende kaarten een symbool kunnen toekennen en dat symbool enkel op die kaarten zetten. En net als bij Dobble wordt dat voor grotere stapels kaarten ondoenlijk, omdat de kaarten veel te veel symbolen zouden bevatten. De uitdaging is dus opnieuw om symbolen meerdere keren te gebruiken en die slim te spreiden over de kaarten.

per combinatie van drie kaarten.
Het kleinste voorbeeld van een interessant blokdesign in die familie wordt meteen al gebruikt voor de groene stapel kaarten in het spel. Het gaat om 8 kaarten met elk 7 symbolen die elk 4 keer voorkomen (terwijl de constructie met een uniek symbool voor elke drie kaarten al 21 symbolen per kaart zou afbeelden). De kaarten kunnen we identificeren met de hoekpunten van een kubus. De blokken komen er grotendeels overeen met vlakken: er zijn drie paren van zijvlakken, drie paren van diagonale vlakken, en nog twee speciale extra blokken (met elk vier hoekpunten die onderling diagonaal liggen langs de kubus). Die in totaal 14 blokken staan hieronder geïllustreerd aan de hand van een toegekend symbool.
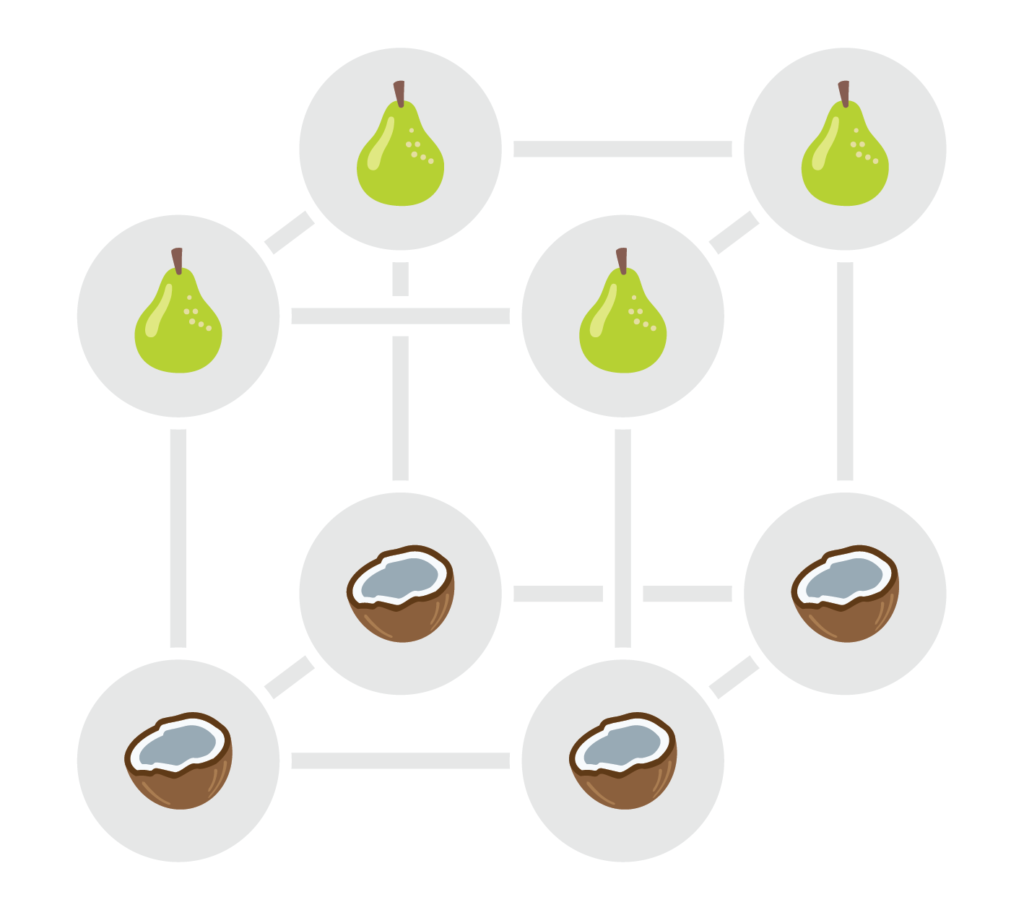
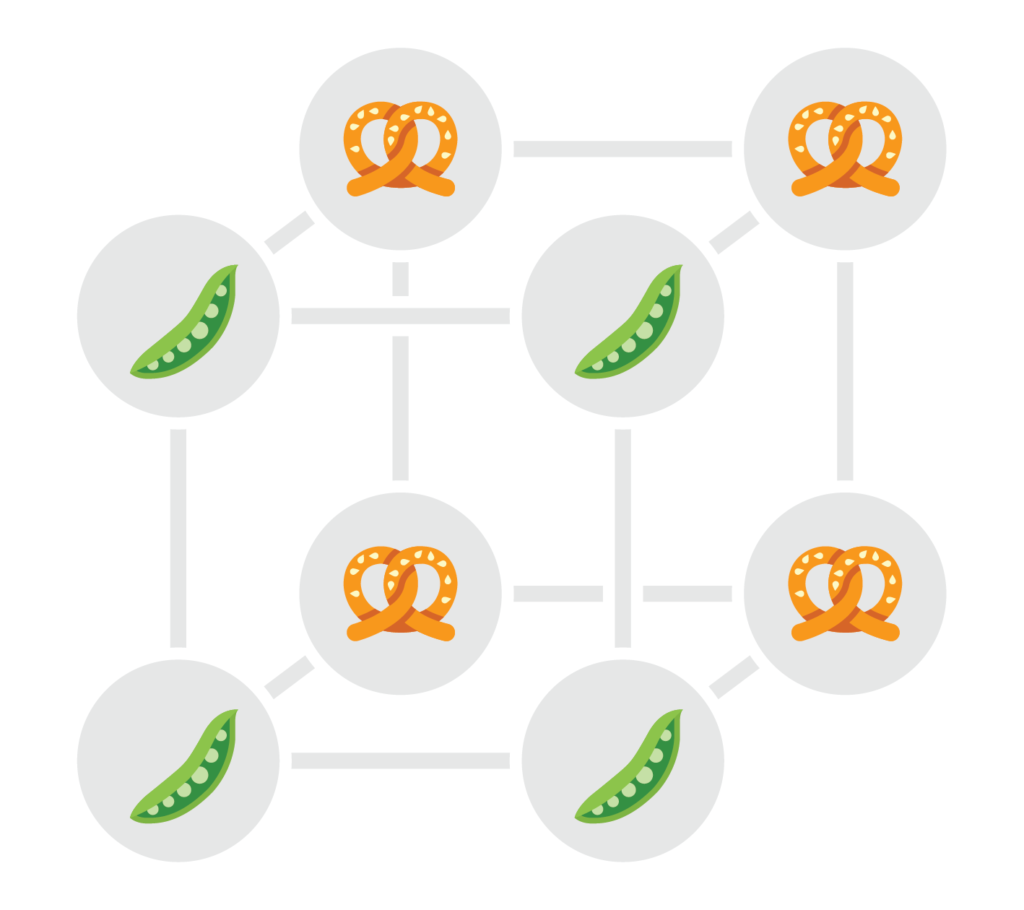

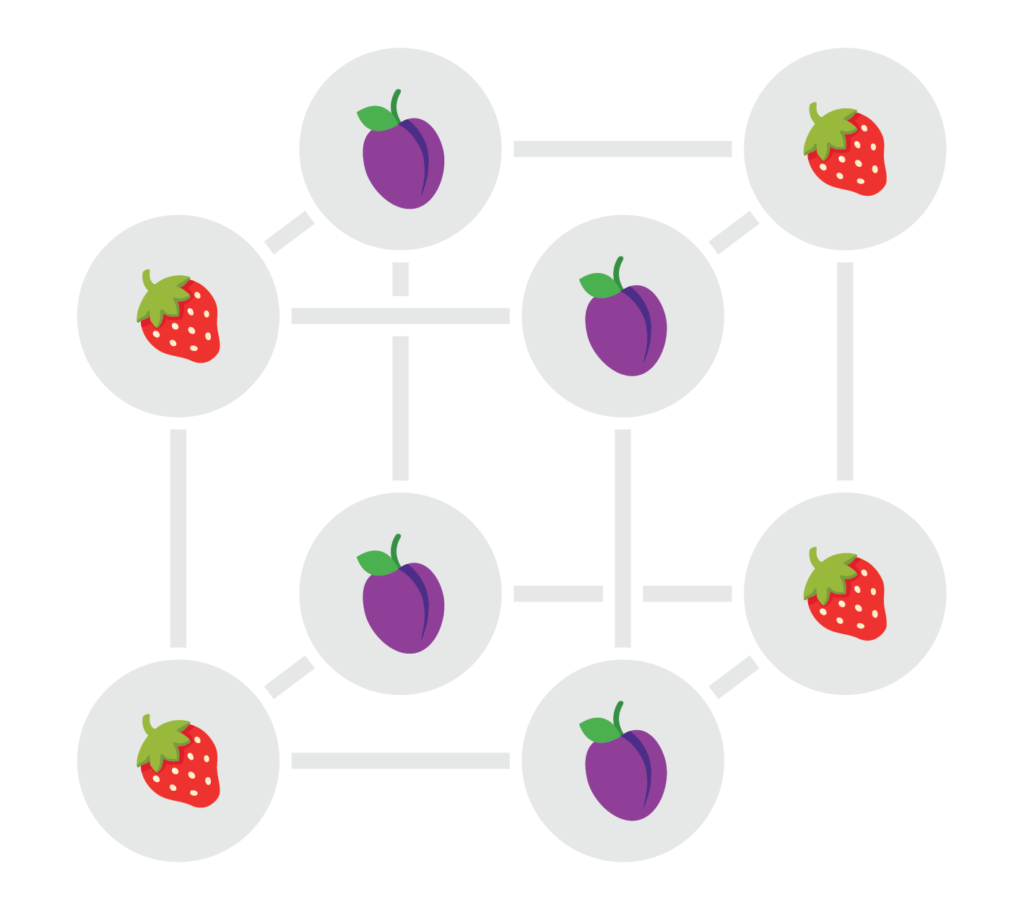
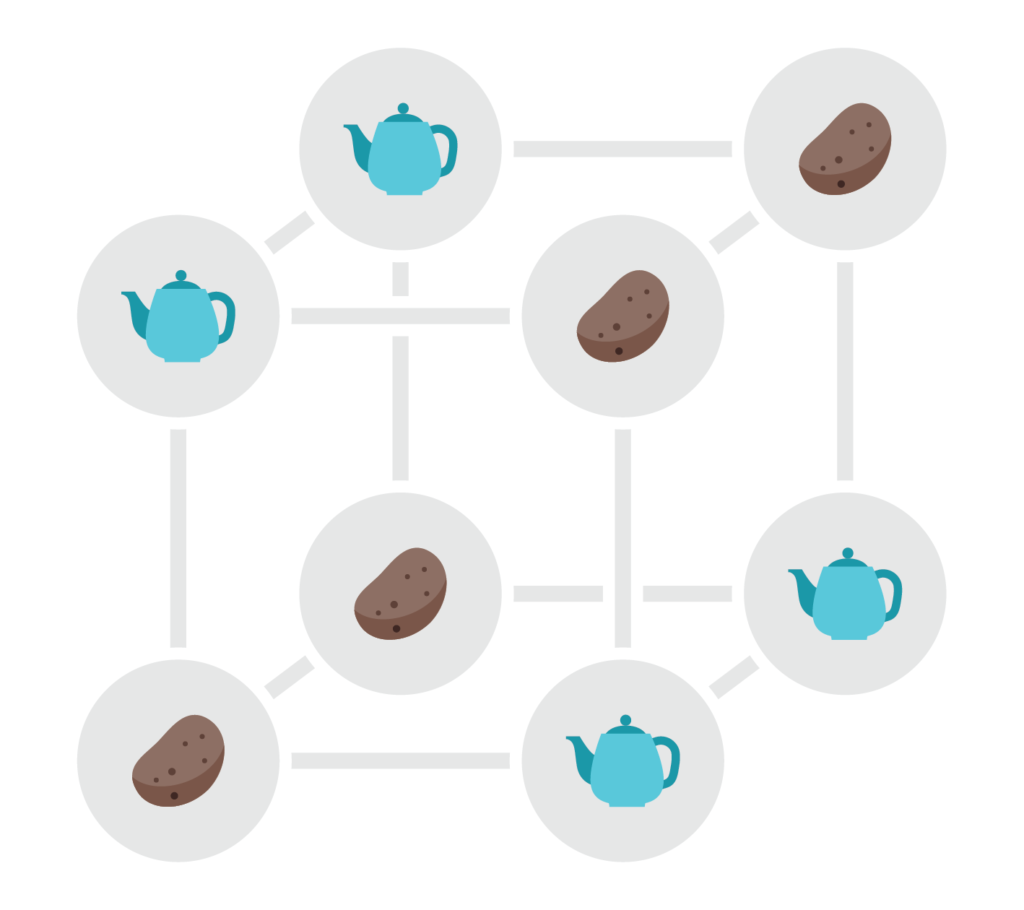
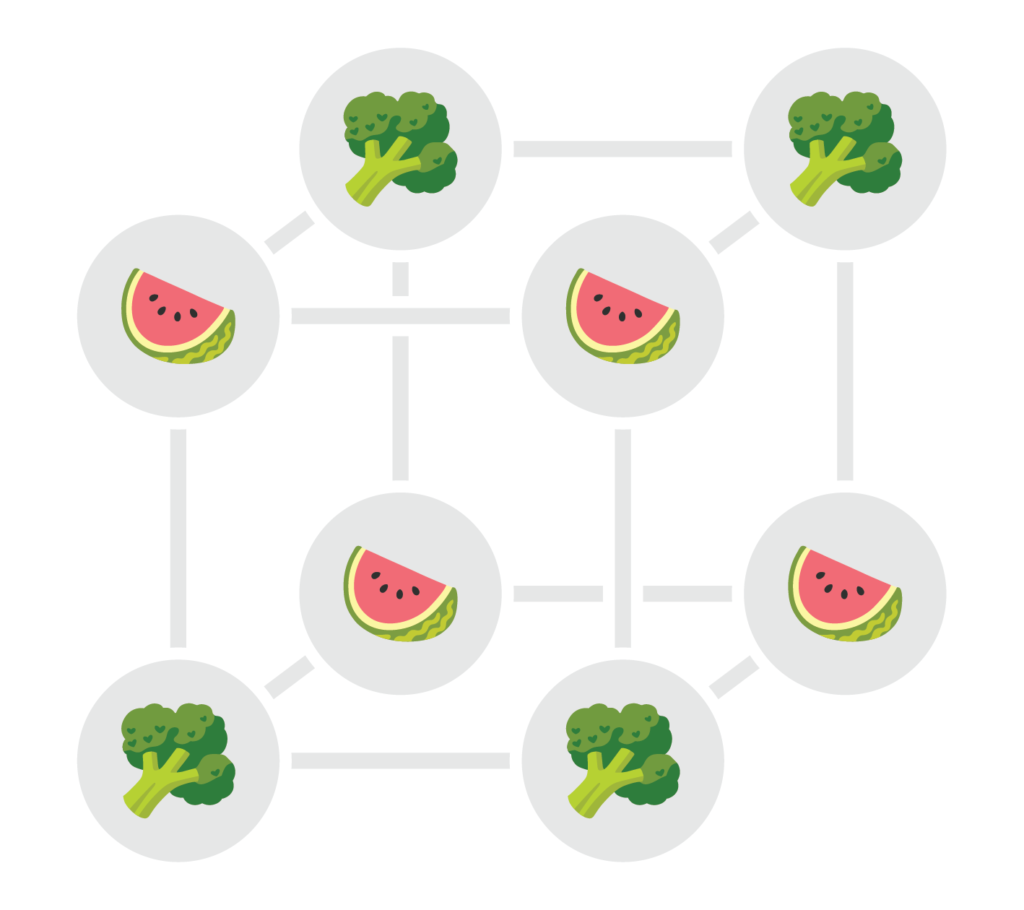
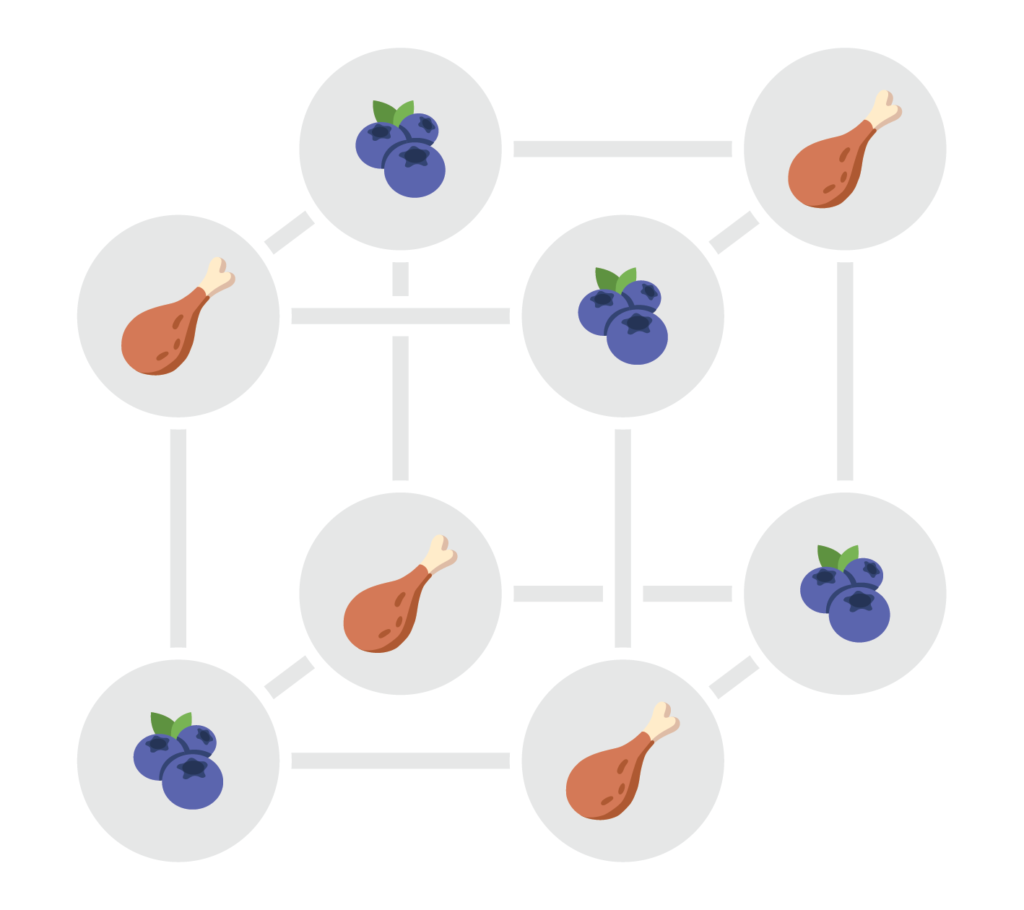
Je kan verifiëren dat eender welke drie hoekpunten van de kubus inderdaad in precies één van die 14 blokken liggen. Ook ligt elk hoekpunt in totaal in precies 7 blokken. De figuur hieronder beeldt de kaarten in hun volledigheid af, ingevuld met alle symbolen corresponderend met de blokken waartoe het punt behoort.
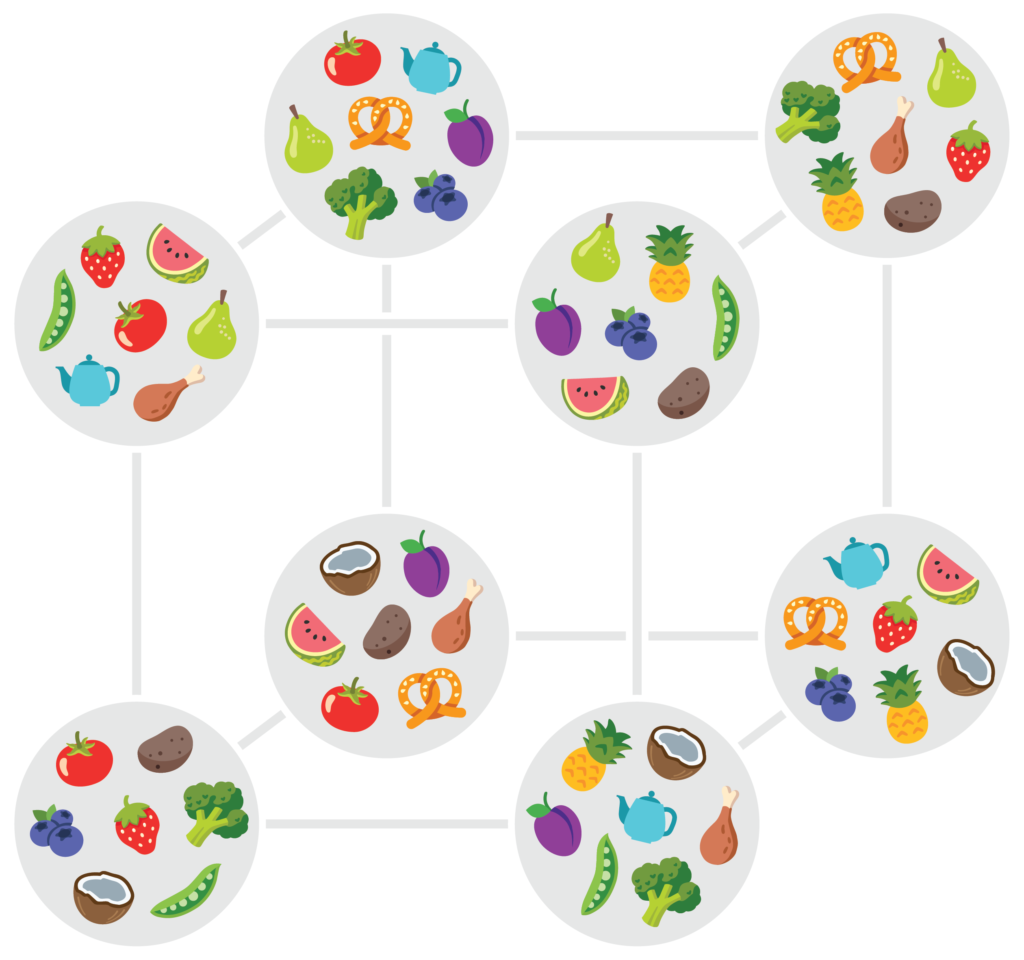
Er zijn 8 kaarten in totaal, 7 symbolen op elke kaart, 4 kaarten die elk gegeven symbool bevatten, 14 verschillende symbolen in totaal. Je kan nagaan dat elke twee kaarten juist 3 gemeenschappelijke symbolen hebben. En — belangrijkst van al — elke drie kaarten hebben juist 1 symbool gemeenschappelijk. Ook bij de grotere sets kaarten in Møbee kun je wat telwerk doen: de rode set bestaat uit 17 kaarten, waarop telkens 20 symbolen staan. Er zijn 68 verschillende symbolen in totaal en elk symbool komt op 5 kaarten voor.
Al die getallen zijn niet gewoon willekeurig te kiezen maar voldoen aan bepaalde wetmatigheden. Zo is het totale aantal symbolen op alle kaarten samen enerzijds gelijk aan [het aantal verschillende symbolen] vermenigvuldigd met [het aantal kopieën van elk symbool], maar anderzijds ook aan [het aantal kaarten] vermenigvuldigd met [het aantal symbolen per kaart]. Inderdaad, 14 × 4 = 8 × 7 in de eerste set, en 68 × 5 = 17 × 20 in de tweede set. Maar er schuilen nog veel meer verborgen relaties.
Steinersystemen
De blokdesigns waarop Møbee gebaseerd is, zijn voorbeelden van Steinersystemen. Opnieuw doen hier enkele variaties de ronde maar de moderne definitie beschrijft die in termen van drie parameters: een Steinersysteem \(S(t,k,n)\) is een verzameling van \(n\) punten, samen met blokken van elk \(k\) punten groot, zodat elke \(t\) punten samen in precies één blok voorkomen. Om saaie gevallen uit te sluiten, kunnen we eisen dat \(k\geq 4\). Het kleinste Møbeespel is bijvoorbeeld geconstrueerd uit een Steinersysteem \(S(3,4,8)\), en de andere twee zijn \(S(3,4,10)\) en \(S(3,5,17)\). In speltermen staat \(n\) voor het aantal kaarten, komt elk symbool in totaal op \(k\) kaarten voor, en moet \(t=3\) om te voldoen aan de Møbee-eigenschap.
In functie van die parameters kun je heel wat andere belangrijke getallen berekenen, zoals het totale aantal blokken door één punt, oftewel het aantal symbolen op één kaart. Noem dat aantal \(r\). We kunnen een formule voor \(r\) opstellen door een kaart vast te kiezen en op twee verschillende manieren te tellen hoe we die kunnen uitbreiden naar een lijst van drie kaarten. Enerzijds kun je de symbolen negeren: kies gewoon een arbitraire tweede kaart uit de \(n-1\) andere in de stapel en dan een derde uit de \(n-2\) overblijvende kaarten. Anderzijds zal er precies één gemeenschappelijk symbool op de drie gekozen kaarten staan. Je kan dus evengoed eerst een van de \(r\) symbolen op de kaart kiezen, daarna een tweede kaart uit de andere \(k-1\) kaarten met datzelfde symbool, en dan een derde uit de \(k-2\) overblijvende kaarten met dat symbool. Omdat die twee tellingen hetzelfde resultaat moeten geven, volgt dat \((n-1)\cdot(n-2) = r\cdot(k-1)\cdot(k-2)\), of anders gezegd,
\[r = \frac{(n-1)\cdot(n-2)}{(k-1)\cdot(k-2)}.\]
We kunnen controleren dat die klopt voor de Møbeekaarten: in \(S(3,4,8)\) komen er 7 symbolen voor op elke kaart, en inderdaad: \(7 = \frac{7\cdot 6}{3\cdot 2}\). Vind je ook de juiste getallen in \(S(3,4,10)\) en \(S(3,5,17)\)?
Nog een belangrijke parameter is \(b\), het totale aantal blokken (of symbolen) in het Steinersysteem \(S(3,k,n)\). Met een gelijkaardige dubbele telling van het aantal manieren om drie kaarten te kiezen (zonder een vaste kaart), volgt dat \(n\cdot(n-1)\cdot(n-2) = b \cdot k\cdot(k-1)\cdot(k-2)\), of anders gezegd,
\[b = \dfrac{n\cdot(n-1)\cdot(n-2)}{k\cdot(k-1)\cdot(k-2)}.\]
Opnieuw geeft die het juiste resultaat voor Møbee — in \(S(3,4,8)\) komen er totaal 14 symbolen voor, en \(14 = \frac{8\cdot 7\cdot 6}{4\cdot 3\cdot 2}\). Controleer zelf even: hoeveel verschillende blokken/symbolen zijn er in \(S(3,4,10)\) en \(S(3,5,17)\)?
Het doosje van Møbee komt met drie stapels van 8, van 10 en van 17 kaarten groot. Die laatste is ineens best wat groter dan de kleinere twee, dus misschien kunnen we op zoek gaan naar een extra stapel met 13 kaarten, bijvoorbeeld in een Steinersysteem \(S(3,5,13)\). De formules leren ons dat \(r=11\), dus er zouden 11 symbolen op elke kaart staan. Maar als je het totale aantal symbolen narekent, dan zou \(b=\frac{143}{5}\). Aangezien het om een aantal gaat, zou dat natuurlijk een geheel getal moeten zijn! Dat betekent dat een Steinersysteem met die parameters gewoon niet kan bestaan. De twee formules voor \(b\) en \(r\) vormen best sterke restricties om Steinersystemen te kunnen construeren.
Toch zijn ook hier oneindig grote families gekend. Zo is er een best technische constructie (in eindige driedimensionale projectieve meetkundes) die Steinersystemen oplevert met parameters \(S(3,q+1,q^2+1)\) voor elke priemmacht \(q\). Voor \(q=2\) is dat het Steinersysteem \(S(3,3,5)\) en dat is net een van die saaie gevallen. Voor \(q=3\) verkrijgen we \(S(3,4,10)\) en voor \(q=4\) verkrijgen we \(S(3,5,17)\) — twee die in het spel Møbee voorkomen! Bovendien worden die constructies Möbiusvlakken genoemd, en daar komt ook de naam Møbee vandaan.
Ook het kleinste systeem \(S(3,4,8)\) behoort tot een oneindige familie. Zo bewees Haim Hanani in 1960 al (2) dat een Steinersysteem van de vorm \(S(3,4,n)\) met \(n\geq 5\) bestaat voor elke \(n\) in \(\{8,10,14,16,20,22,\ldots\}\) (even getallen die geen veelvoud van 6 zijn) en niet voor andere \(n\).
Opnieuw is het verhaal hier nog niet gedaan. De Steinersystemen relevant voor Møbee hebben allen parameter \(t=3\) en Dobble is gebouwd op designs met \(t=2\), maar ook voor grotere waarden van \(t\) zijn er tal van interessante designs te bestuderen … die opnieuw vertaald kunnen worden naar een spel met symbolen en kaarten. Bovendien zijn er varianten die bijvoorbeeld precies twee gemeenschappelijke symbolen op elke twee of drie kaarten krijgen (op een interessante manier). In de volgende blogpost gaan we daar verder op in. Wordt vervolgd!


