Begin oktober 2023 vond SPIEL Essen plaats in Duitsland, een vierdaagse bordspellenbeurs en tevens de grootste ter wereld. Ik was een van de 193 000 aanwezigen en zocht er enthousiast naar obscure of splinternieuwe spellen met een wetenschappelijk kantje. Een van de spellen waar ik bijvoorbeeld naar uitkeek was Quirky Quarks, aangekondigd als een spel waarin je biedt op subatomaire deeltjes. Maar de grootste ontdekking was toch wel een spel in de prototypehal waar nog nauwelijks buzz rond hing, genaamd Møbee. Ik was meteen dolenthousiast, stond er een uur lang te praten met de ontwerper en bleef ook nadien nog in contact. Je kan Møbee intussen ook op onze webshop vinden — een primeur buiten het thuisland Hongarije.
Maar waarom deed het spel mijn wiskundehart een slag overslaan? Wel … daarvoor moeten we eerst kijken naar een ander spel genaamd Dobble, een spel dat intussen erg populair is geworden, in zowat elke speelgoedwinkel te vinden is en waarvan tal van herinkledingen zijn uitgebracht.
Dobble: de spelregels
Dobble (of Spot it!) is een kaartspel met 55 ronde kaarten waarop telkens 8 symbolen staan. Er zijn een aantal spelvarianten, maar het komt er telkens op neer dat er twee kaarten worden omgedraaid en de spelers zo snel mogelijk het symbool moeten vinden dat op die twee kaarten staat. Het spel is zó gemaakt dat elke combinatie van twee kaarten juist één symbool gemeenschappelijk heeft. Wie dat symbool het snelst vindt, krijgt een punt, en er worden nieuwe kaarten omgedraaid.
Over de spelregels valt niet zoveel meer te zeggen: je hebt ze in tien seconden beet, het is toegankelijk voor jong en oud, en een potje Dobble is ook in enkele minuten uitgespeeld.
Naast de originele Dobble zijn er tal van speciale edities gemaakt, zoals Dobble Belgium met allemaal Belgische symbolen, maar ook junior- of teamversies met meer of minder symbolen op de kaarten.

Dobble: de constructie
Waar er wél heel veel meer achter schuilt, is de constructie van de kaarten. Hoe kun je een set kaarten ontwerpen met die cruciale Dobble-eigenschap dat elke twee kaarten juist één symbool gemeenschappelijk hebben? Je kan gewoon wat proberen en er zelfs de computer bijhalen om systematisch alle mogelijkheden te overlopen, maar bedenk dat dat aantal mogelijkheden snel gigantisch wordt en dat je steeds meer en meer restricties ziet om nieuwe kaarten toe te voegen die met alle vorige kaarten compatibel zijn. Gelukkig zijn er ook inzichtelijkere manieren.
Er zijn enkele saaie constructies die een set kaarten met de Dobble-eigenschap opleveren. Je kan bijvoorbeeld gewoon één symbool kiezen, die op elke kaart zetten, en alle kaarten opvullen met enkele symbolen die nergens anders voorkomen. Flauw natuurlijk, want dan is er weinig spel meer aan. Een iets minder saaie manier is om een symbool te kiezen voor elke combinatie van twee kaarten en dat symbool enkel op die twee kaarten te gebruiken. Dat werkt op zich perfect, tot je even uitrekent hoeveel symbolen er op elke kaart staan. Wel, één symbool voor elke andere kaart natuurlijk … Met andere woorden, voor de 55 kaarten van de officiële Dobble zouden er zo 54 symbolen op elke kaart staan (en 1 485 verschillende symbolen in totaal). Da’s net iets te overweldigend voor een aangenaam familiespel.

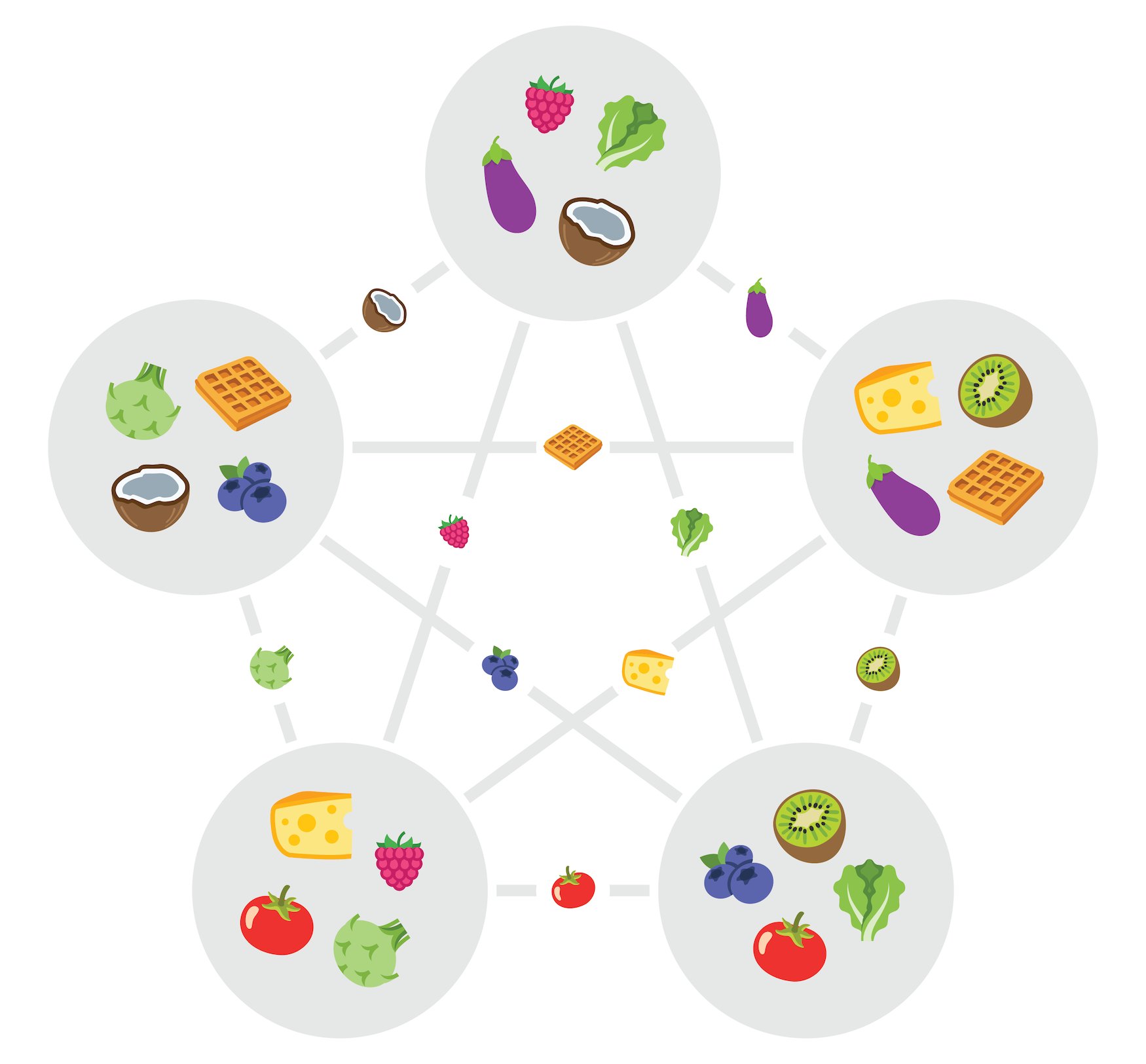
Om zo’n absurd grote kaarten te vermijden, moeten symbolen meerdere keren voorkomen dan op slechts twee kaarten. Wie even wil natellen zal in een Dobbleset acht kopieën van een symbool terugvinden over alle kaarten. Dan blijft de vraag natuurlijk: hoe verdeel je die systematisch over de kaarten zodat die de gewenste Dobble-eigenschap vertonen?
Door klein te beginnen kun je na wat knutselen misschien een set opstellen van zeven kaarten, telkens met drie symbolen erop, waarbij elk symbool al drie keer voorkomt (in plaats van slechts twee keer). De achterliggende structuur is gekend onder wiskundigen als het Fanovlak. Het wordt een “vlak” genoemd omdat het doet denken aan meetkunde, met punten en rechten: de kaarten kun je interpreteren als punten, die op eenzelfde rechte liggen als ze hetzelfde symbool delen. De rechten door een punt corresponderen met andere woorden met de symbolen op de kaarten.
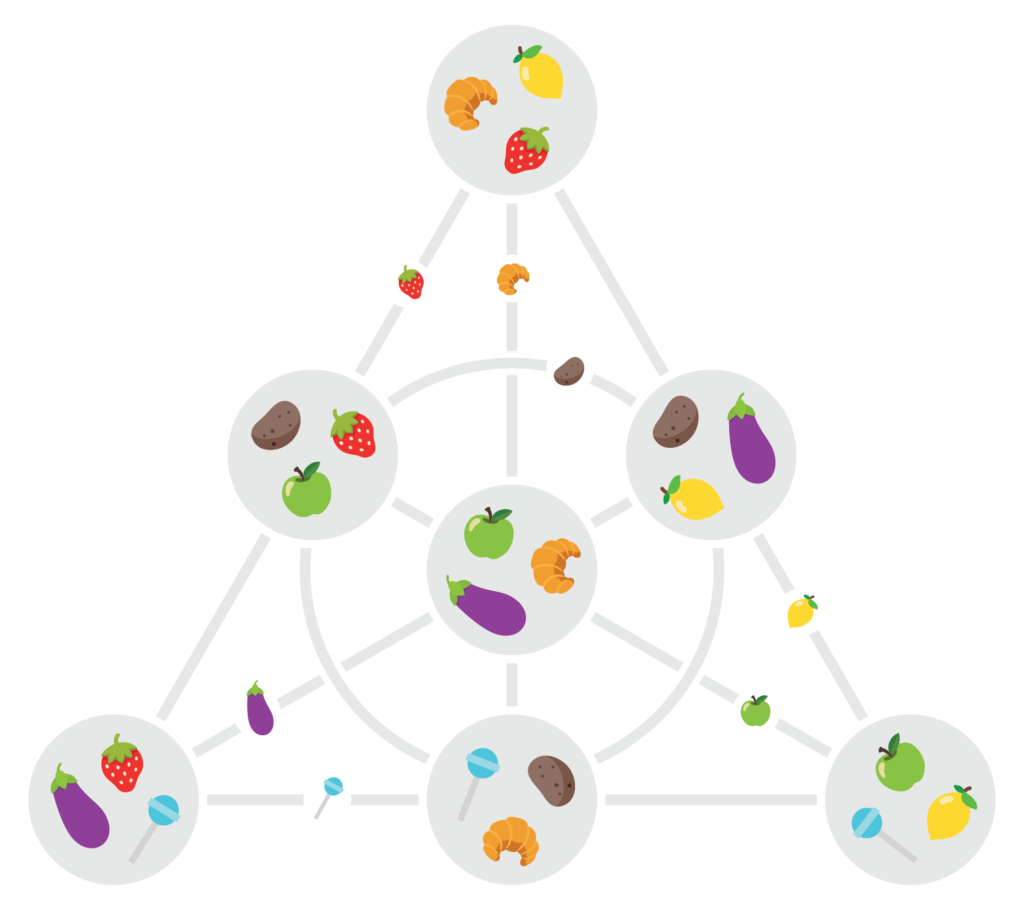
Ook de Dobble-eigenschap klinkt heel natuurlijk in een meetkundige context: “elke twee kaarten hebben een symbool gemeenschappelijk” betekent dat elke twee punten verbonden moeten zijn door juist één rechte. Dat is een eigenschap waarmee we zodanig vertrouwd zijn in onze klassieke meetkunde dat we er zelfs niet langer bij stilstaan. Toch zijn er ook heel wat opvallende verschillen in het Fanovlak. Zo liggen er niet meer dan drie punten op een rechte, en zijn er in totaal niet meer dan zeven punten en zeven rechten — dat maakt het een voorbeeld van een eindige meetkunde. Ook opvallend: er bestaan geen evenwijdige rechten in het Fanovlak, want élke twee rechten snijden in juist één punt — dat maakt het een voorbeeld van een projectief vlak. In Dobbletermen betekent dat laatste dat elk paar van twee symbolen ergens op een en hetzelfde kaartje voorkomt.
Laat je niet vangen door de tekening: net omwille van die ongewone eigenschappen is het lastig om zo’n eindig projectief vlak “waarheidsgetrouw” te tekenen. Tussen de kaartjes liggen geen andere punten op de rechten, en de centrale “cirkel” is wel degelijk een rechte met drie punten zoals alle andere. Een weergave van het Fanovlak waarin alle rechten effectief recht zijn, bestaat niet.
Het Fanovlak geeft een speelbare miniversie van Dobble, maar is nog verre van een interessant spel. Daarvoor hebben we een grotere achterliggende meetkunde nodig met meer rechten door elk punt (i.e. meer symbolen op elke kaart). Gelukkig bestaan er ook grotere eindige projectieve vlakken. Eén stap groter bijvoorbeeld (met vier symbolen per kaart) kun je als volgt te werk gaan. Begin met een rooster van 3 bij 3 punten. Teken drie horizontale rechten, drie verticale rechten, en twee keer drie schuine rechten rondom het rooster, en ken die elk al een symbool toe zoals hieronder. Elke twee punten zijn zo al verbonden door juist één rechte. Door de vier figuren boven elkaar te leggen, verkrijg je alvast een geldige Dobbleset van negen kaarten met vier symbolen op elke kaart.
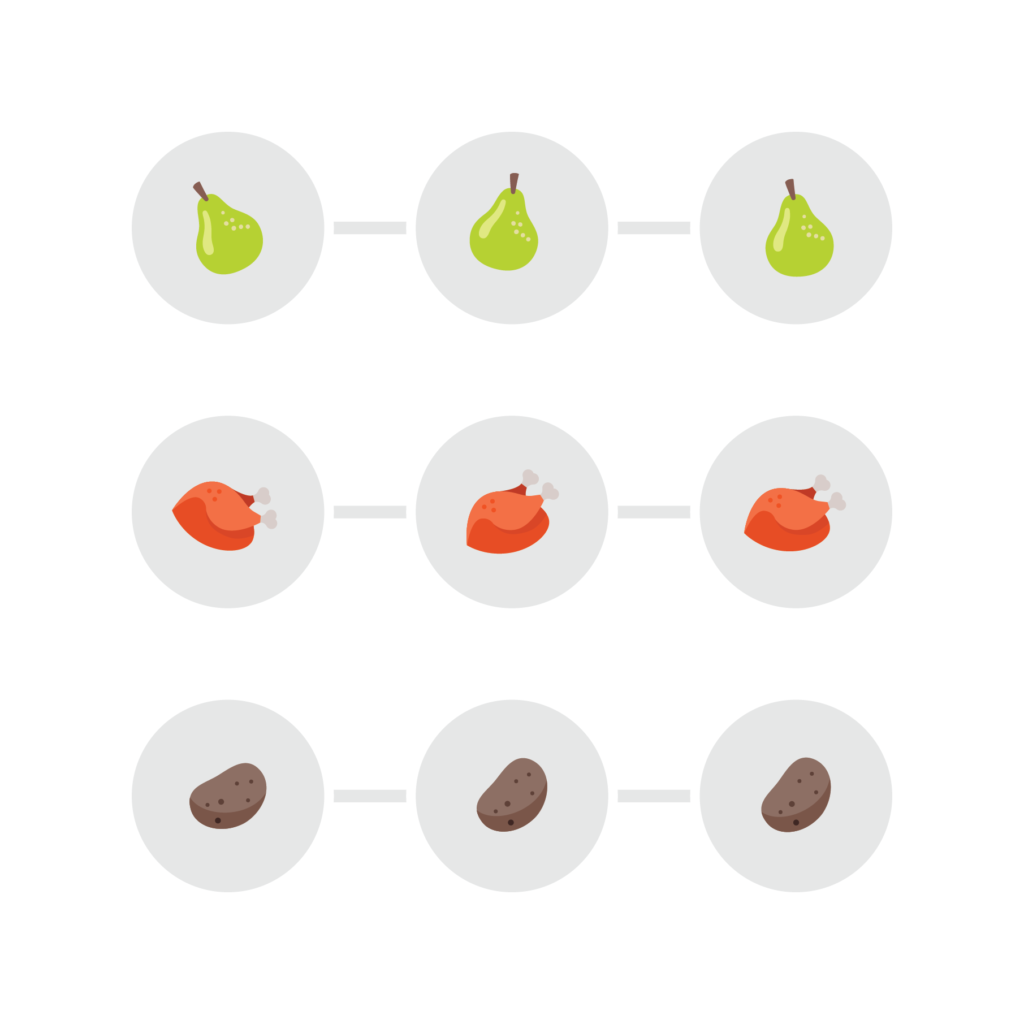
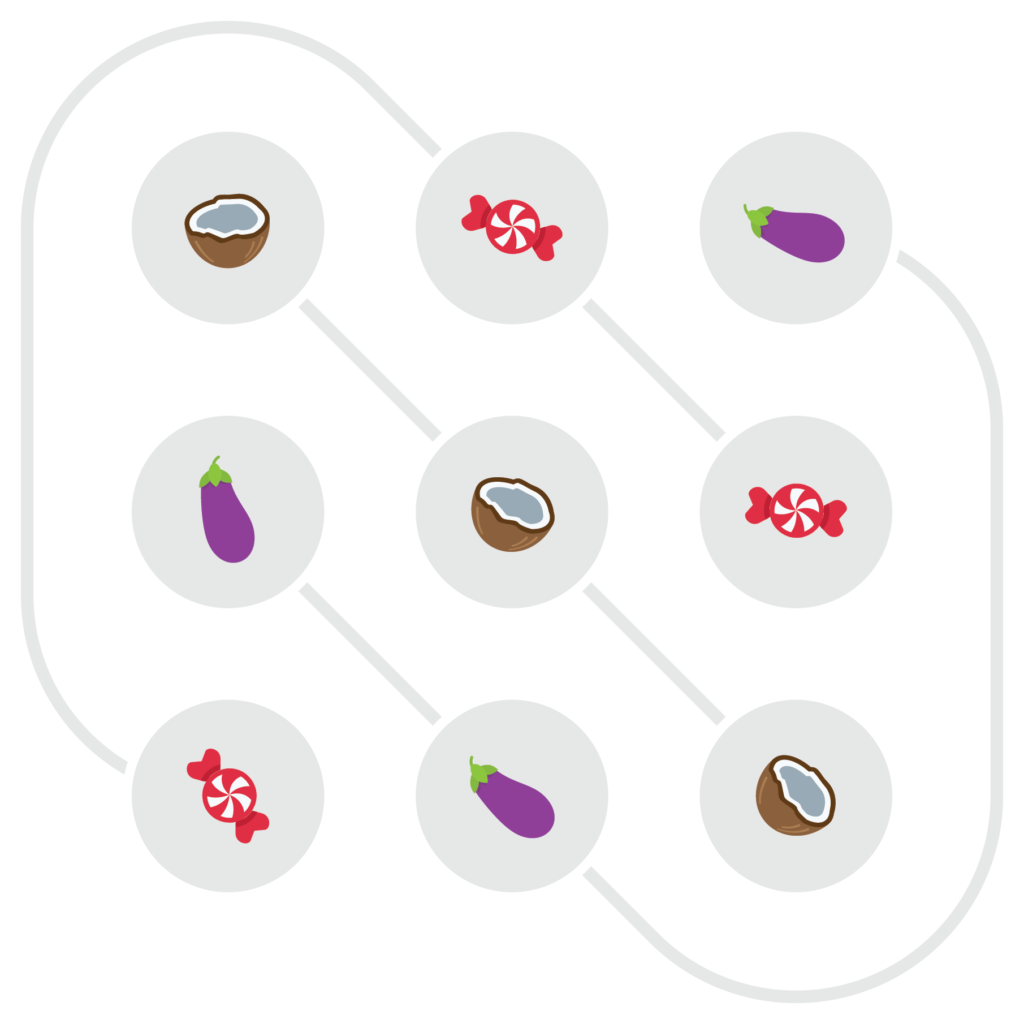

Maar het kan nog iets beter. In de huidige constructie zijn er nog evenwijdige rechten, die geen punten gemeenschappelijk hebben (het is een voorbeeld van een eindig affien vlak). Anders gezegd, er zijn nog combinaties van twee symbolen die niet samen op een kaart voorkomen. Op zich geen probleem — de set kaarten in hun huidige vorm is perfect speelbaar — maar je kan nog vier extra kaarten toevoegen door een “rechte op oneindig” toe te voegen, met de vluchtpunten van de evenwijdige rechten. Die kaarten op oneindig bevatten elk de symbolen van drie evenwijdige rechten, plus een extra symbool corresponderend met de rechte op oneindig zelf. Zo eindig je opnieuw met een projectief vlak met 13 punten, een set Dobblekaarten waarin ook elke mogelijke combinatie van symbolen op een kaart te vinden is en die dus niet verder uit te breiden is.

Het Fanovlak hierboven kun je met precies dezelfde techniek opbouwen: begin met een rooster van 2 bij 2 punten, teken de horizontale, verticale en schuine rechten, en voeg de drie punten op oneindig toe voor een totaal van zeven punten. De klassieke weergave van het Fanovlak verhult die constructie ten gunste van een symmetrischere figuur. Ook voor het vlak met 13 punten zijn er andere weergaves zoals die hieronder.
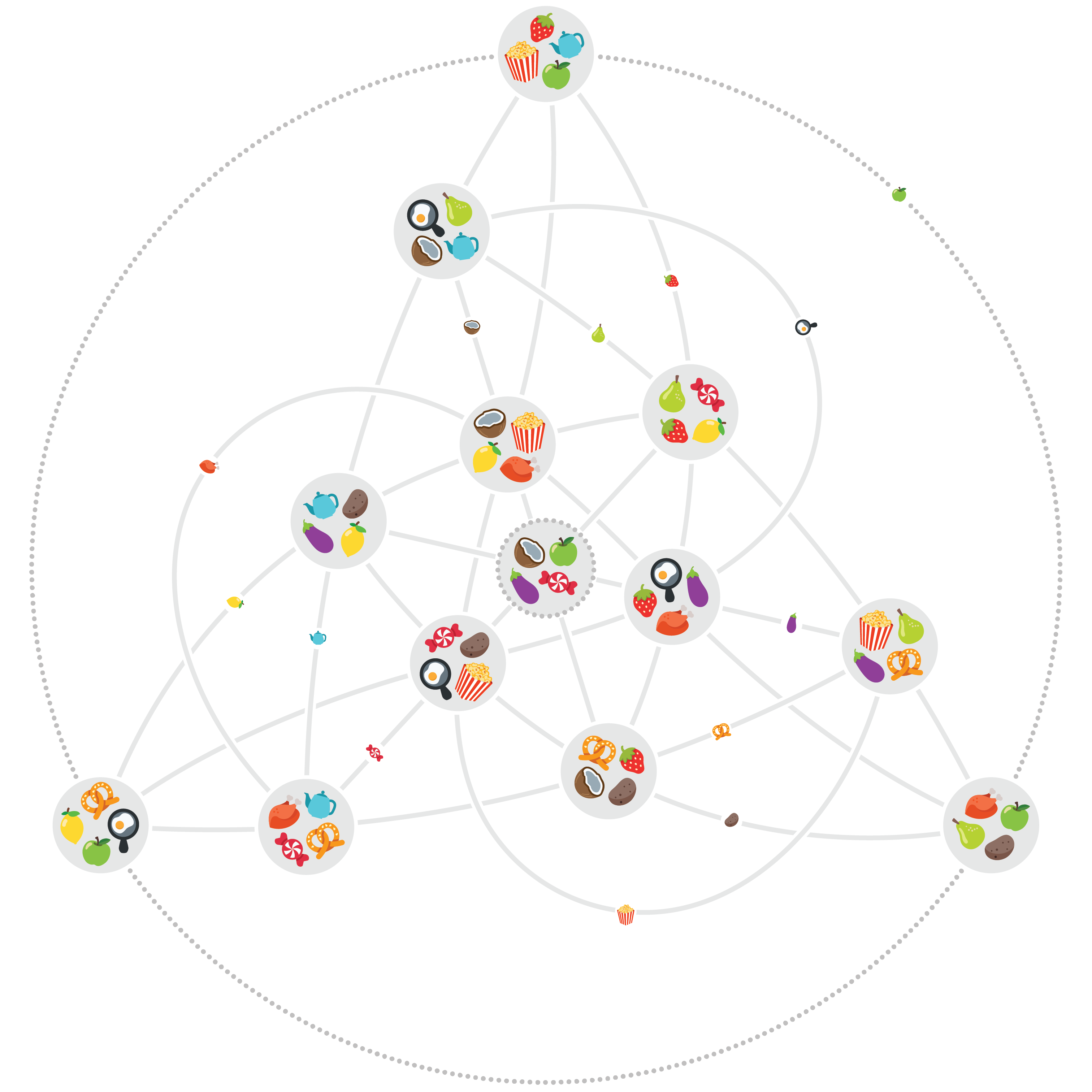
Projectieve vlakken worden ingedeeld volgens hun orde. Zo heeft het Fanovlak orde 2 en het vlak hierboven orde 3. Die orde is niet het aantal punten per rechte (het aantal symbolen op elke kaart) maar ééntje minder. Op die manier verwijst de orde naar de grootte van het initiële rooster, wat het vergelijken van affiene en projectieve vlakken makkelijker maakt.
Met een gelijkaardige constructie vanuit een rooster kun je nog grotere projectieve vlakken opbouwen … maar enkel wanneer de orde een priemgetal is! Bij een samengesteld getal vullen de schuine rechten in het rooster immers niet langer mooi alle punten op maar overlappen die, wat zou betekenen dat rechten in meerdere punten snijden. In Dobbletermen zou dat kaarten opleveren die meerdere symbolen gemeenschappelijk hebben!

Gelukkig is die priemrestrictie voor Dobble geen probleem. Het klassieke Dobblespel heeft acht symbolen op elke kaart en komt inderdaad overeen met een projectief vlak van orde 7 — een priemgetal. De juniorversie heeft zes symbolen op elke kaart en is geknutseld uit een projectief vlak van orde 5 — opnieuw priem. Opvallend genoeg zijn beide versies eigenlijk niet compleet: classic Dobble komt met 55 kaarten, maar het volledige vlak van orde 7 heeft 57 punten (en evenveel rechten). Ook de juniorversie komt met 30 kaarten in plaats van het theoretische maximum van 31. Waarom juist is niet officieel bevestigd, maar heeft wellicht te maken met productiekosten en/of marketing.
De grotere teamversie van Dobble is echter wel nog een verklaring verschuldigd, want die heeft orde 9 — geen priemgetal! Ook al loopt de constructie vanuit een 9-bij-9-rooster spaak, toch bestaat er een andere manier om aan een projectief vlak van die orde te geraken, steunend op een expliciet systeem van een exotisch soort coördinaten. Die methode kan een projectief vlak genereren met een willekeurige priemmacht als orde: 2, 3, 4, 5, 7, 8, 9, 11, 13, 16, 17, 19, 23, 25, 27, 29 …
Een ronduit schitterende video over de wiskunde achter Dobble is die van Matt Parker op zijn YouTubekanaal Stand-up Maths (1). Daarin maakt hij niet alleen de constructie van een projectief vlak duidelijk met animaties, maar komt ook een volledig andere manier naar boven om een set Dobblekaarten te genereren aan de hand van zogenaamde difference sets. Natuurlijk is dat niet toevallig: er zijn al lang vele raakvlakken gekend tussen projectieve vlakken en andere combinatorische configuraties zoals die difference sets (2). Matt Parker vertelt in zijn video ook over allerlei varianten van Dobble en een spel genaamd Catch the Match — een aanrader.
Fijn is dat Dobble geen geheim maakt van de wiskundige achtergrond: het doosje komt met een korte nota over de geschiedenis en de wiskunde die raakt aan foutverbeterende codes, blokdesigns en een gerelateerde puzzel genaamd het schoolmeisjesprobleem van Kirkman.
Dobble: de open vragen
Hoe zit het met de andere mogelijke ordes? Kunnen we een interessante set Dobblekaarten maken met 13 symbolen op elke kaart? Wel … dat is nog verre van duidelijk.
Gaston Tarry bewees in 1901 dat er geen projectief vlak van orde 6 bestaat, zij het in nog een heel andere context — eigenlijk was hij bezig met een sudoku-achtige opgave, het 36 officierenprobleem van Euler. Van die puzzel vind je een speelbare vorm op onze webshop en meer lezen over de achterliggende wiskunde kun je op deze pagina. Het was Raj Chandra Bose die in 1938 de connectie met meetkunde legde en doorhad dat het resultaat van Tarry het bestaan van projectieve vlakken van orde 6 uitsluit.
De volgende te kraken noot was 10 en die bleek nog heel wat lastiger. Tarry kon orde 6 nog nét met de hand aan, maar voor orde 10 is dat ronduit ondoenlijk. Doorheen de jaren 80 werd de kwestie beslecht door middel van een kolossale computerzoektocht. Clement Lam geeft een uitstekend verslag (3) over de geschiedenis van het probleem en in het bijzonder het titanenwerk dat orde 10 vroeg.
Zo bevredigend is een computerbewijs niet echt — ook al weten we dat een projectief vlak van orde 10 niet bestaat, een overtuigende reden waarom is er niet. Zelfs het bewijs van Tarry voor orde 6 kwam min of meer neer op een zorgvuldig overlopen van alle mogelijkheden en verifiëren dat geen enkele “werkt”. Er zijn wel enkele algemene structurele resultaten gekend die wat meer inzicht verschaffen, zoals de stelling van Bruck–Ryser. Die legt een bepaalde numerieke restrictie op de orde en sluit op die manier meteen heel wat potentiële ordes (4) uit, waaronder 6 en 14. Maar zelfs orde 12 is op dit moment nog een mysterie. Zo’n hypothetisch vlak zou “slechts” 157 punten en evenveel rechten moeten hebben, oftewel 157 Dobblekaarten met 13 symbolen per kaart, maar zelfs met de krachtigste hedendaagse computers is die volledig buiten bereik!
- Stand-up Maths, How does Dobble (Spot it!) work? (↩)
- Gerald Berman, Finite projective plane geometries and difference sets. Transactions of the American Mathematical Society, vol. 74, 1953, p. 492–499. (↩)
- Clement W. H. Lam, The search for a finite projective plane of order 10. The American Mathematical Monthly, vol. 98, no. 4, 1991, p. 305–318. (↩)
- Online Encyclopedia of Integer Sequences, A046712. (↩)


