Een eindje geleden berichtten we over de ontdekking van de einstein: een langgezocht figuurtje dat het vlak betegelt, maar enkel en alleen zonder (globale) herhaling. Wij staken dolenthousiast de lasercutter aan het werk om enkele honderden exemplaren uit te snijden en puzzelden gretig vele leuke vormpjes ineen. De einsteinmicrobe sloeg snel over naar vrienden en collega’s die er vele koffiepauzes lang naar hartelust mee speelden.
Juist door het ontbreken van die herhaling bleek het een verrassend pittige opgave om zonder hulp de betegeling samen te leggen. Een geschenk uit de hemel voor onze puzzelstand op Nerdland Festival dus! We sneden opnieuw enkele honderden stukken uit, dit keer in wat groter formaat en uit dikker 6 mm mdf. Omdat we deze graag als een van de eyecatchers op onze stand wilden presenteren, gaven we die nog wat kleur: we schilderden de ene kant roze, de andere kant paars. We schreven ook een (uitgebreide!) bundel achtergrondinformatie voor erbij.


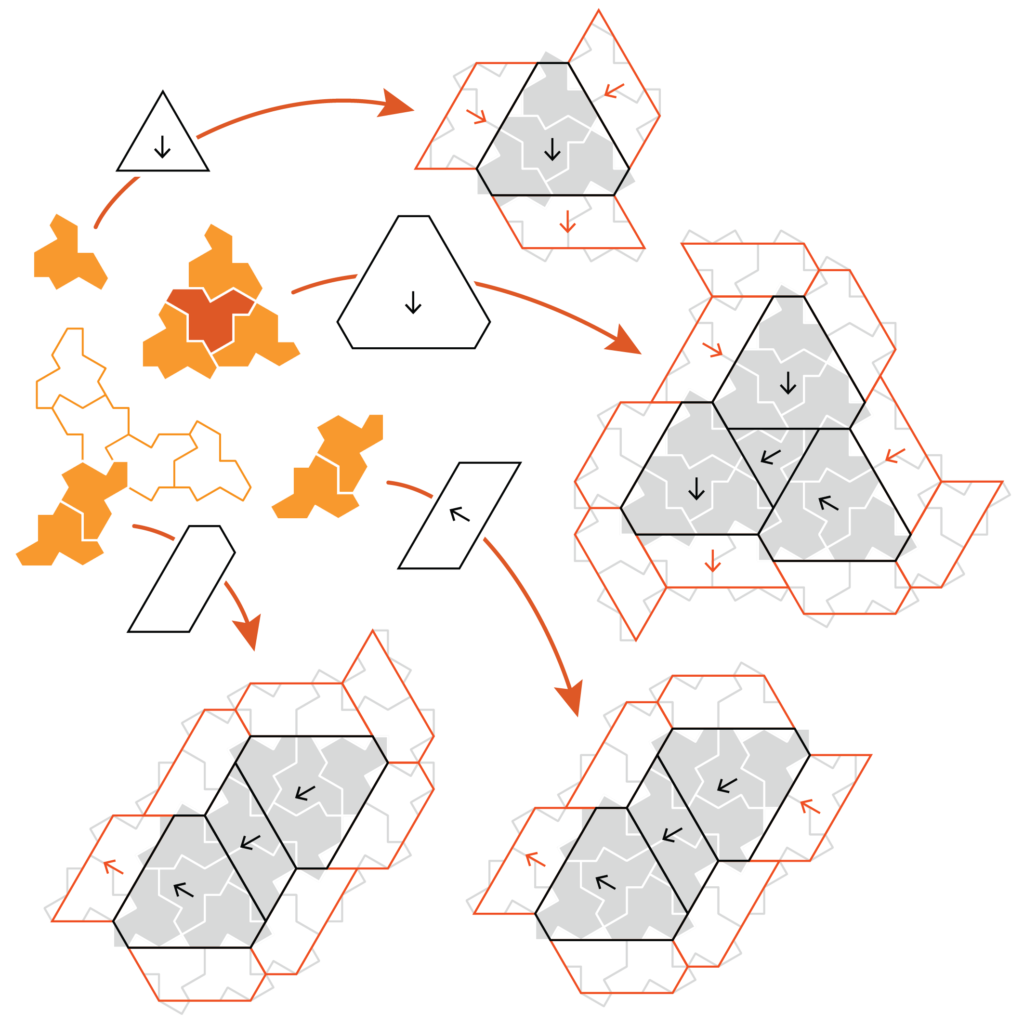
In die bundel vertellen we onder meer waarom de betegeling juist aperiodiek is, weliswaar schetsmatig natuurlijk. Een cruciaal ingrediënt is de vaststelling dat de stukjes slechts op bepaalde manieren in elkaar passen. In de uiteindelijke driehoek herken je een aantal patronen: driehoekige bouwstenen in twee groottes, gelegen tussen spaakachtige structuren. De onderzoekers David Smith, Joseph Samuel Myers, Craig Kaplan en Chaim Goodman-Strauss (1) toonden met computerzoektochten aan dat het figuurtje alleen volgens die bouwstenen in elkaar past en dat er eigenlijk ook maar één manier is om die stapsgewijze uit te breiden. Het bouwplan hieronder geeft een indicatie hoe dat in z’n werk gaat: een enkel tegeltje kan worden “opgeblazen” naar een viertal in een driehoekige vorm, die vervolgens alleen maar kan worden opgeblazen naar een grotere combinatie driehoekjes omgeven door spaken, die …
Dat bouwplan is ook voor een andere reden nuttig. Als je héél goed oplet, dan kun je zien dat de figuur in twee oriëntaties voorkomt: op de figuur links staan de grijze en lichtoranje tegels met dezelfde kant naar boven, maar de donkeroranje liggen ondersteboven (oftewel, werden gespiegeld). Met behulp van enkele wiskundige technieken kun je dan berekenen hoeveel tegels uiteindelijk zo ondersteboven liggen. Dat aantal blijkt net geen 15%, of om precies te zijn \((\varphi-1)^4\) met \(\varphi\) de gulden snede!
Die andersom georiënteerde tegels geven de twee kleuren op onze puzzelstukken een significante meerwaarde. Een uitgebreid verslag van onze bevindingen bij onze puzzels op Nerdland Festival volgt binnenkort, maar we delen alvast mee dat de kleuren tot verrassende en leuke effecten leidden tijdens het vele gepuzzel met de einstein, ook bij creatievere invullingen van de opgave.

Anderzijds … zijn de twee oriëntaties niet een beetje een schoonheidsfoutje? Herinner je dat het einsteinprobleem vroeg naar één enkele tegel die uitsluitend aperiodiek betegelt. Tegels soms ondersteboven leggen, is dat dan geen valsspelen? Ik hoorde iemand het een eineinhalbstein noemen, een anderhalfsteen, in plaats van een echte einstein. Is er ook een vormpje dat enkel aperiodiek betegelt zonder reflecties?
Laat die vervolgvraag nu nét opgelost worden tijdens Nerdland Festival! Jawel, zondag 28 mei deelde hetzelfde team een preprint (2) waarin ze ook die puzzel kraakten. Met andere woorden, de vele uren schilder- en lakwerk hadden we kunnen halveren, want er is nu ook een vormpje gekend dat maar langs één kant naar boven ligt.
De nieuwe versie werd uit de gekende einstein geknutseld door in eerste instantie alle zijden even lang te maken. Die nieuwe vorm is niet meer zomaar uit een mooie opdeling van zeshoeken af te leiden, maar past toch nog steeds op meerdere manieren ineen: in dezelfde aperiodieke configuratie als de originele einstein, maar ook op een periodieke manier. Die beide configuraties vereisen dat het stukje ook ondersteboven wordt gepuzzeld. Zoals de onderzoekers ontdekten, is er echter nog een andere manier waarbij alle stukjes in dezelfde oriëntatie liggen … en die is aperiodiek. Wanneer reflecties a priori verboden worden, is de enige mogelijkheid nog een aperiodieke betegeling.
De laatste stap in de constructie is dan om alle zijden te vervangen door een randje dat forceert dat stukken in dezelfde oriëntatie aansluiten. Denk bijvoorbeeld aan twee uitsteeksels links en rechts van elke zijde, die ondersteboven niet langer matchen. Er is bovendien een beetje speling mogelijk want zo’n randje hoeft niet volledig symmetrisch te zijn — een asymmetrisch fragmentje volstaat ook, op voorwaarde dat die alternerend naar binnen en naar buiten langs de rand van de nieuwe tegel wordt gelegd.
Na zelf wat experimenteren met leuke vormen langs de rand, blijkt een driehoekig kantje met hoeken van 30°, 60° en 90° best esthetische resultaten te geven. Omdat de hoeken van de originele einstein veelvouden waren van 30° blijft dat zo voor de gemodificeerde vorm. Er zijn vier mogelijkheden om de zijden zo aan te passen; in de variant links valt met wat fantasie een draak of dinosaurus te herkennen, rechts een wandelende kameel. De draak spreekt mij het meeste aan! Wat herken jij in de tegels, en welke is jouw favoriet?
- David Smith, Joseph Samuel Myers, Craig Kaplan, Chaim Goodman-Strauss, An aperiodic monotile. ArXiv:2303.10798. (↩)
- David Smith, Joseph Samuel Myers, Craig Kaplan, Chaim Goodman-Strauss, A chiral aperiodic monotile. ArXiv:2305.17743. (↩)