Blog

Opmerking: deze blogpost is een vervolg op de post over Dobble en die over Møbee — meer specifiek, over de meetkunde die achter die spellen schuilt — en bouwt dan ook verder op enkele begrippen zonder die opnieuw in te voeren.

Herinner je je het populaire spel Dobble en de verrassende meet­kundige structuur die erachter schuilt? In deze blogpost kijken we naar een gerelateerd reactie­spel dat eveneens alom­tegen­woordig te vinden is in menig speelgoed­winkel en waar tot op vandaag nog serieus wiskundig onderzoek naar wordt gevoerd: het kaartspel SET.

SET: de spelregels

De spelregels van SET zijn een stukje complexer dan die van Dobble. SET komt met 81 kaarten, waarop telkens een aantal symbolen staan met een aantal karakteristieken. De kaarten komen in drie kleuren: rood, groen en paars. Ook komen de symbolen voor in variërende aantallen: enkel, dubbel of driedubbel. Er zijn drie vormen: rond, ruitvormig, of gegolfd. En tot slot zijn er drie manieren van opvullen: leeg, gearceerd of ingevuld. Er zijn niet toevallig juist 3 × 3 × 3 × 3 = 81 manieren om die karakteristieken te combineren — elke mogelijke combinatie komt juist ergens met een kaart overeen.

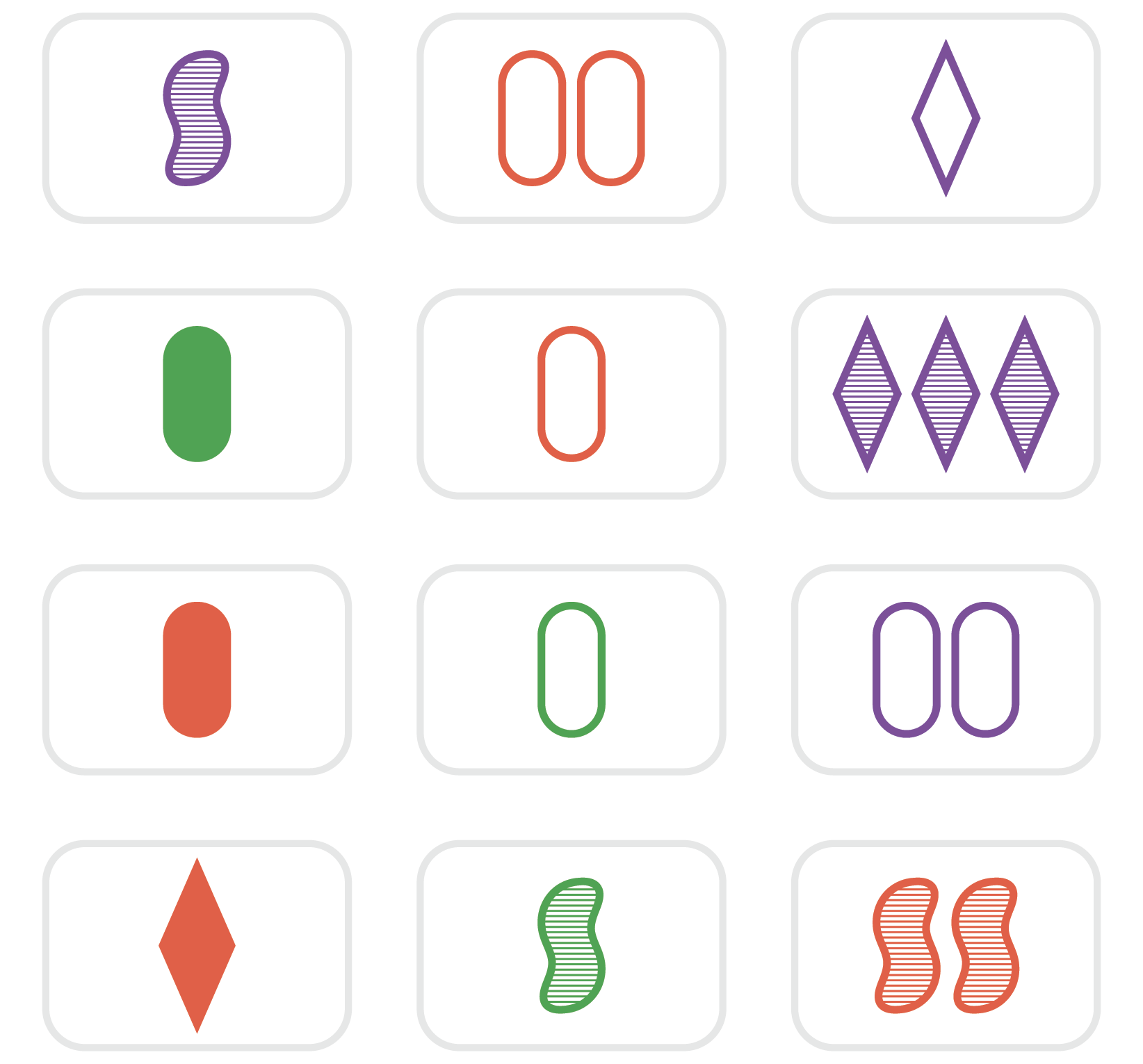
Een SET bestaat nu uit drie kaarten die voor elk van de vier afzonderlijke karakteristieken, ofwel drie keer dezelfde optie vertonen, ofwel juist de drie verschillende opties. Een trio van drie rode kaarten of van een kaart in elk kleur kan bijvoorbeeld een SET vormen (als ook de andere karakteristieken kloppen) maar twee rode kaarten samen met een paarse kaart vormt zeker geen SET. Hieronder enkele voorbeelden van geldige SETs.

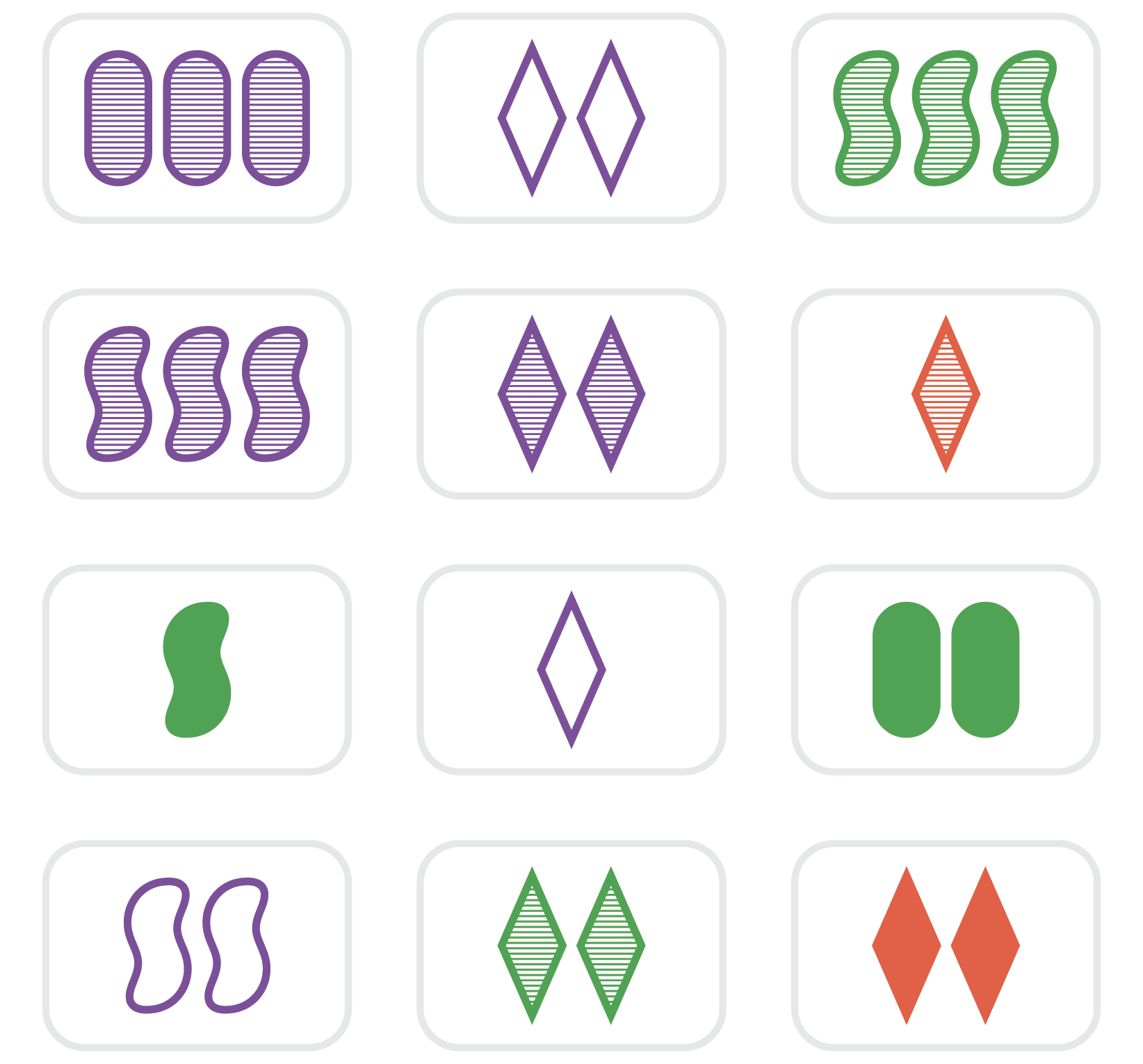
Hoe speel je nu een potje SET? Schud de 81 kaarten en leg er twaalf open zoals hieronder. De spelers zoeken zo snel mogelijk naar een SET. Wie een gevonden heeft, roept “SET” en neemt de drie kaarten bij zich (samen goed voor een punt). Drie nieuwe kaarten worden open­gedraaid en de zoektocht naar een nieuwe SET begint. Het spel eindigt na het delen van de laatste kaarten en het scoren van de laatste punten.

Vaak zijn er meerdere SETs te vinden in twaalf kaarten (de verwachtingswaarde is 2,78). Soms kan het echter gebeuren dat er geen enkele SET ligt. In dat geval worden uitzonderlijk drie nieuwe kaarten omgedraaid. Na het vinden van een SET gaat het spel weer verder met twaalf kaarten.

Om het herkennen van een SET nog wat in de vingers te krijgen, kun je de officiële dagelijkse puzzel proberen of je wagen aan de pittige opgaven hieronder. De volgende observatie kan helpen om systematisch af te zoeken: gegeven eender welke twee kaarten bestaat er telkens slechts één unieke kaart die de SET vervolledigt. Zo moet een paarse en een groene kaart immers worden aangevuld met een rode kaart, of twee groene kaarten met een derde groene kaart, en op dezelfde manier liggen ook de andere karakteristieken van de derde kaart vast.

De geschiedenis van het spel is best opmerkelijk! De ontwerper van SET is populatiegeneticus Marsha Jean Falco, die in 1974 onderzoek deed naar epilepsie bij Duitse herders­honden (1). Al zoeken naar patronen in de genetische data van de honden kreeg ze het idee om die beknopt voor te stellen als abstracte symbolen op kaarten. Falco realiseerde zich dat ze een uitdagend puzzel­spel vasthad, en SET was geboren! Het idee althans, want ook al werd het spel een succes onder vrienden en kennissen, een eerste commerciële versie werd pas jaren later op de markt gebracht in 1991.

SET: de constructie

Net als bij Dobble schuilt er veel meer structuur in de 81 kaarten van SET dan je op het eerste zicht zou denken. Om eenvoudig te beginnen, bekijk even 9 kaarten die op twee karakteristieken volledig hetzelfde zijn, zoals hieronder qua kleur (rood) en qua aantal (enkel). Die passen samen in een rooster­vormige figuur die je misschien nog herkent van de Dobble­constructie en die een eindig affien vlak wordt genoemd.

De SETs in dit minispel komen precies overeen met de rechten in het affien vlak: er zijn drie horizontale rechten van kaarten met dezelfde vulling, drie verticale rechten van kaarten met dezelfde vorm, en twee keer drie schuine rechten met gemengde karakteristieken.

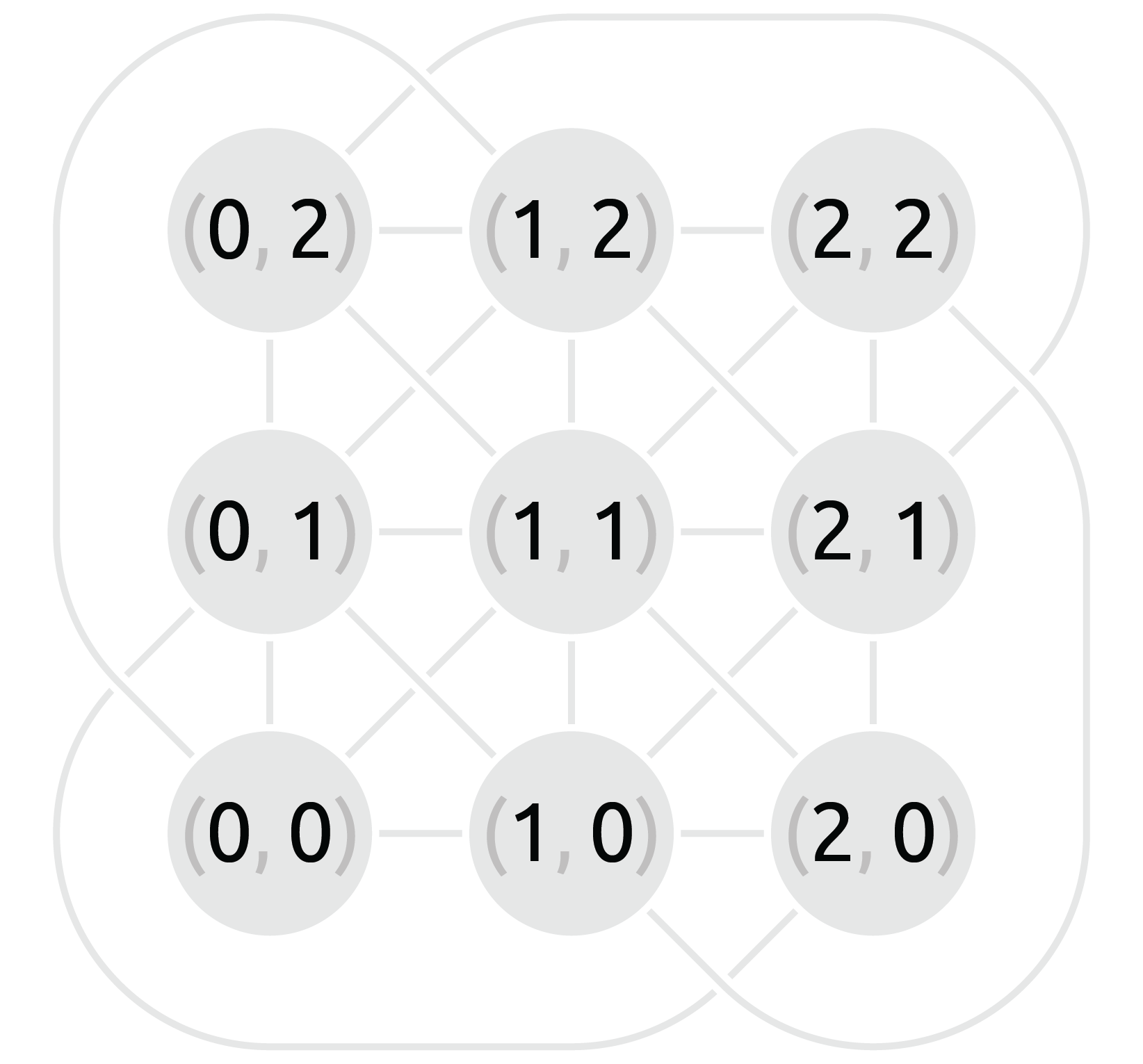
Abstracter kun je elke kaart op de figuur beschrijven met twee coördinaatgetallen, eentje voor elke karakteristiek — hier is 0 = afgerond, 1 = ruitvormig, 2 = gegolfd voor de eerste coördinaat, en 0 = opgevuld, 1 = gearceerd, 2 = leeg voor de tweede coördinaat. Een geldige SET heeft niet zomaar willekeurige coördinaat­getallen. Voor elke karakteristiek zijn de mogelijkheden immers ofwel 0 + 0 + 0 ofwel 1 + 1 + 1 ofwel 2 + 2 + 2 ofwel 0 + 1 + 2, en dat zijn precies de mogelijkheden om een veelvoud van 3 als som te verkrijgen.

Als we er een derde karakteristiek bijnemen, dan passen de in totaal 27 kaarten in een driedimensionale kubus­vormige structuur met telkens drie coördinaten. Dat spel werd ook effectief uitgegeven onder de naam SET Junior. De samenhang van de volle 81 kaarten in SET valt moeilijk herkenbaar te tekenen, maar de beschrijving in termen van vier coördinaatgetallen (en dus vier dimensies) werkt precies hetzelfde: drie kaarten vormen een SET als de vier sommen van hun vier coördinaatgetallen elk een veelvoud zijn van 3.

Deze meetkunde achter SET is een eindige affiene ruimte (van dimensie 4). Het feit dat elke twee kaarten met een unieke derde kaart tot een SET kunnen worden uitgebreid, betekent meetkundig dat elke twee punten op juist één rechte liggen. Typerend aan deze meetkunde is daarnaast het optreden van evenwijdigheid of parallellisme : elke gegeven SET verdeelt op een natuurlijke manier de overblijvende kaarten in evenwijdige SETs.

Affiene meetkunde mag misschien onschuldig ogen, toch zijn er heel wat lastige en zelfs onopgeloste onderzoeksvragen te stellen. Zo komt het bijvoorbeeld niet vaak voor dat een speelveld van twaalf kaarten geen enkele SET bevat — met kans 3,23% — maar over de loop van een potje SET passeren er veel kaarten de ronde en is het waarschijnlijk dat er wel eens drie extra kaarten moeten worden omgedraaid. Zijn die drie extra kaarten voldoende om zeker een SET te kunnen vinden? Wel … het blijkt van niet. Een collectie kaarten zonder ook maar één SET wordt een kap genoemd. In 1970 vond Guiseppe Pellegrino zo’n kap van grootte 20 (2), en hij toonde aan dat dat het maximum is: het bestaan van een SET is dus pas gegarandeerd bij 21 of meer kaarten! Hieronder vind je een voorbeeld van een SET-loze 20 kaarten. Merk op dat dit resultaat, in abstracte meetkundige termen, al enkele jaren gekend was vóór Falco met het idee voor SET op de proppen kwam.

Niets houdt je tegen om groter te gaan dan vier karakteristieken in je SET-spel. Wij hebben drie identieke dozen in de spellenkast liggen en denken nog altijd na over een manier om die netjes samen te voegen tot een SuperSET van 243 kaarten (bijvoorbeeld met een letter S, E of T op de hoekjes van de kaarten). Het is geweten dat je in zo’n vijfdimensionaal spel een kap van 45 SET-loze kaarten kan vinden. Nog een stap verder kun je uit 729 kaarten met zes karakteristieken een selectie maken van 112 zonder SET. Hoe de lijst juist verder gaat, is nog niet goed begrepen (3). Er zijn onder- en boven­grenzen gekend, maar er wordt nog steeds actief onderzoek gedaan naar manieren om die scherper te krijgen.

Nog een laatste leuk weetje: wij spelen altijd een kleine variant van SET, waarin de allerlaatste kaart van de stapel niet wordt open­gedraaid. Nee hoor, je hoeft echt niet alle andere 80 kaarten te hebben onthouden om die laatste te kunnen afleiden! Wel kun je steunen op de coördinaten: voor elke karakteristiek is de som van alle 81 coördinaat­getallen een veelvoud van 3 (concreet 81) en elke weggenomen SET doet die som afnemen met een veelvoud van 3 (concreet 0, 3 of 6). Op het einde van het spel moet die som van de overblijvende kaarten dus nog steeds een veelvoud van 3 zijn en zo kun je de karakteristiek van de laatste kaart afleiden. Stel bijvoorbeeld dat er nog 9 kaarten overblijven, waaronder 4 paarse kaarten, 2 groene en 2 rode, dan moet de laatste kaart wel paars zijn. Zo niet is er onderweg een fout gebeurd bij het verklaren van een SET!

De schoolmeisjespuzzel van Kirkman

In de vorige blogpost over Møbee kwamen blok­­designs (en in het bijzonder Steiner­systemen) al ter sprake. Ook SET kunnen we zien als zo’n Steiner­systeem: het volledige spel SET is juist \(S(2,3,81)\), bestaande uit \(n=81\) kaarten opgedeeld in verscheidene blokken (rechten) van \(k=3\) kaarten. Parallellisme geeft hier een interessante extra eigenschap aan de blokken: de collectie van alle blokken kan worden opgedeeld in families van “evenwijdige” blokken die op hun beurt mooi de punten­verzameling overdekken, zonder overlappen. Een blokdesign dat voldoet aan die bijzondere bijkomende evenwichts­oefening wordt oplosbaar (resolvable) genoemd.

Affiene ruimten geven dus aanleiding tot oplosbare blokdesigns maar er zijn zeker ook andere te vinden. Zo is er een beroemde puzzel — het school­meisjes­probleem van Kirkman — die in feite vraagt om het oplosbare Steiner­systeem \(S(2,3,15)\) op te stellen. Thomas Kirkman publiceerde zijn opgave in 1850 in The Lady’s and Gentleman’s Diary in de vorm hieronder; er zijn meerdere oplossingen te vinden, steunend op verschillende meet­kundige constructies (4).

Fifteen young ladies in a school walk out three abreast for seven days in succession:
it is required to arrange them daily so that no two shall walk twice abreast.

Vijftien schoolmeisjes gaan zeven dagen op wandeling, telkens in rijen van drie.
Hoe zorgen we ervoor dat elk meisjes slechts één keer samen met elk ander meisje wandelt?

Ada – Bea – Cho Dot – Els – Flo Gia – Hay – Isa Jil – Kim – Lot Mia – Nel – Ona

Ada – Dot – Gia Bea – Els – Hay Cho – Jil – Mia Flo – Kim – Nel Isa – Lot – Ona

Ada – Els – Ona Bea – Isa – Jil Cho – Dot – Nel Flo – Hay – Lot Gia – Kim – Mia

Ada – Isa – Mia Bea – Dot – Lot Cho – Els – Kim Flo – Gia – Ona Hay – Jil – Nel

Ada – Flo – Jil Bea – Kim – Ona Cho – Gia – Lot Dot – Hay – Mia Els – Isa – Nel

Ada – Hay – Kim Bea – Gia – Nel Cho – Flo – Isa Dot – Jil – Ona Els – Lot – Mia

Ada – Lot – Nel Bea – Flo – Mia Cho – Hay – Ona Dot – Isa – Kim Els – Gia – Jil

Wiskundige probleempjes in dit genre zijn ook in praktijk erg nuttig! Vervang de wandelende meisjes bijvoorbeeld door spelers die het tegen elkaar opnemen in een toernooi. Wat kennis van blokdesign­theorie laat toe om efficiënte toernooien te organiseren waarin iedereen juist één keer tegen elke tegenstander speelt en waarbij iedereen tegelijk kan beginnen aan de volgende match. Als we ooit een SET-toernooi organiseren, dan hopen we alvast op een opkomst van 15 of 27 spelers!

1. M. Falco, J. Barker, M. Wallace, The genetics of epilepsy in the British Alsatian. Journal of Small Animal Practice, vol. 15, no. 11, 1974, p. 685–692. (↩)
2. G. Pellegrino, Sul massimo ordine delle calotte in S_4,3. Le Matematiche, vol. 25, 1970, p. 149–157. (↩)
3. Online Encyclopedia of Integer Sequences, A090245. (↩)
4. Marco Pavone, On the seven non-isomorphic solutions of the fifteen schoolgirl problem. Discrete Mathematics, vol. 346, no. 6, 2023. (↩)