Een beetje puzzelliefhebber heeft ongetwijfeld al een puzzel zien passeren waarbij je enkele vormen zodanig in een opgegeven rooster moet passen dat je in de niet-bedekte velden de datum van vandaag kan aflezen. Er doen enkele variaties de ronde. Zo is er een versie met enkel de 31 dagen en 12 maanden, maar ook een versie met daarenboven nog de 7 weekdagen. Voor zover ik weet, bestond er echter nog geen enkele variant die een ander rooster gebruikt dan het eenvoudige vierkante schaakbordpatroon. Zou er ook een gelijkaardige puzzel mogelijk zijn op een ander rooster, zoals een zeshoekig honingraatpatroon? Spoiler alert: ja, en hoe!
Na wat experimenteren blijkt dat de 7 + 31 + 12 = 50 benodigde vakjes mooi ineenpassen in een zeshoekige vorm zoals hieronder, met 3, 4, 5, 6, 7, 7, 6, 5, 4 en 3 vakjes per lijn. Beter nog, de eerste twee lijnen (3 + 4) bevatten precies zoveel vakjes als weekdagen, en de laatste drie (5 + 4 + 3) zoveel vakjes als maanden. Na deze observatie kan ik het idee natuurlijk niet meer loslaten — dit is gewoon te mooi om te negeren, niet?
De uitdaging is uiteraard om een set van puzzelstukjes te vinden waarmee elke combinatie van weekdag, dagnummer en maand een oplosbare puzzel vormt. De mogelijke puzzelstukjes in kwestie heten polyhexen. Ze zijn weliswaar iets minder bekend dan hun vierkante broertjes (de polyomino’s) maar zeker interessant genoeg om even op in te gaan.
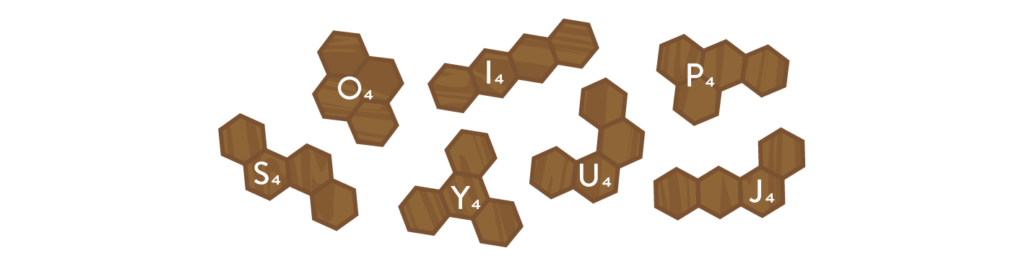
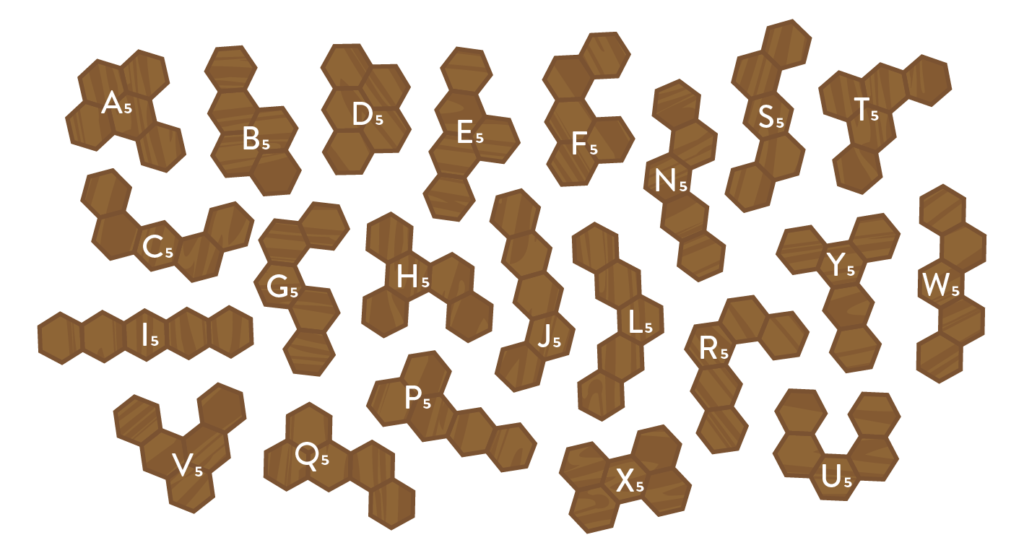
Er is natuurlijk maar één enkel op zichzelf staand zeshoekje, en een tweede zeshoekje eraan plakken kan maar op wezenlijk één manier. Voor drie zeshoekjes zijn er al meer mogelijkheden: recht aan elkaar, in een hoek van 120°, of in een driehoek. De mogelijkheden nemen best snel toe, want er zijn al 7 manieren voor vier zeshoekjes, 22 manieren voor vijf, 82 voor zes, dan 333 … De rij in kwestie is terug te vinden in de On-Line Encyclopedia of Integer Sequences (1) als A000228. Omdat ik de puzzels niet te makkelijk wil maken, negeer ik de kleinste puzzelstukjes en zoek ik naar een set van toffe tetra- en pentahexen, bestaande uit vier of vijf zeshoekjes. Doorheen de puzzelliteratuur worden die 7 en 22 exemplaren met letters aangeduid die (mits enige fantasie) lijken op de vorm van het puzzelstukje.
In totaal bestaat de puzzel uit 7 + 31 + 12 = 50 velden, maar vergeet niet dat er elke dag drie velden onbedekt moeten blijven. Dus, ik zoek een collectie puzzelstukjes met in totaal 47 zeshoekjes. Dat is helaas geen zo’n mooi deelbaar getal, maar 3 tetrahexen en 7 pentahexen kunnen wel werken. Keuze genoeg! Ik probeer allereerst de set {P4, U4, Y4, C5, E5, G5, H5, Q5, T5, X5}, voornamelijk omdat ik de vormpjes wel mooi vind.
Oké … Hoe controleren we nu of de puzzel voor elke datum een oplossing heeft? Natuurlijk niet met de hand, dat is gekkenwerk. Gelukkig bestaan er heel wat computerscriptjes om dit soort puzzels op te lossen. Ik zoek er eentje in een programmeertaal waar ik wat vertrouwd mee ben — uiteindelijk moet ik namelijk niet gewoon één maar wel 7 × 12 × 31 = 2604 puzzels controleren en daar wil ik een loop voor schrijven. Toegegeven, tussen die 2604 data zitten een aantal onmogelijke (zoals 30 februari of 31 september), maar voor het gemak van programmeren wil ik ook die gewoon kunnen oplossen.
De toolkit Polyform Puzzler blijkt precies wat ik nodig heb: geschreven in Python, voldoende flexibel, en met voorziene functionaliteit voor zeshoekige puzzels. Het is natuurlijk even zoeken naar de juiste manier van werken. Eenmaal beet hoe ik mijn tien puzzelstukjes en de vorm dien te definiëren, vindt het scriptje in enkele seconden alle oplossingen (voor één datum). Omdat ik in eerste instantie gewoon geïnteresseerd ben in oplosbaarheid, niet zozeer het aantal oplossingen, stel ik een optie in die het scriptje stopt na één oplossing. Ik pas het vervolgens aan naar een driedubbele geneste lus over alle combinaties en laat het vol spanning lopen.
Een kwartier later zijn alle resultaten binnen. Elke dag blijkt oplosbaar … behalve exact eentje, zaterdag 27 april. Verrassend hoe juist één dag niet lukt, en al de rest wel, maar de conclusie is duidelijk. Het zal je verjaardag maar wezen!
Ik pas één van de kleinere puzzelstukje aan en probeer opnieuw met {J4, U4, Y4, C5, E5, G5, H5, Q5, T5, X5}. Wat blijkt? Hetzelfde verhaal: precies één datum blijkt onoplosbaar, zondag 4 april dit keer. Misschien {J4, U4, Y4, C5, G5, H5, L5, Q5, S5, T5}? Jammer, dinsdag 4 november lukt niet. En schrap {S4, U4, Y4, C5, E5, G5, H5, L5, Q5, T5} maar omwille van zondag 28 februari. De set {I4, O4, U4, C5, D5, E5, I5, L5, U5, Y5} heeft twee vervloekte dagen, donderdag 12 juni en zondag 25 september, elkaars spiegelbeeld in de puzzel. En ook bij {J4, S4, Y4, C5, E5, G5, H5, Q5, T5, X5} lukken zaterdag 3 februari en zondag 4 april niet (dit keer niet elkaars spiegelbeeld). Natuurlijk passeren er ook enkele sets met bijvoorbeeld een 30-tal onoplosbare dagen, maar ik vind het bijzonder verrassend hoe er vaak juist één of twee dagen uit de boot vallen.
Gelukkig vind ik er ook die wél werken — de eerste was {P4, S4, Y4, C5, E5, G5, H5, Q5, L5, X5}. Eindelijk een excuus om onze lasercutter aan het werk te zetten! Ik laat het honingraatpatroon met tekst graveren en de puzzelstukjes in een omliggende vorm uitsnijden uit 3 mm dik mdf. Het graveren neemt een kwartiertje tijd in beslag, het snijden gaat een pak sneller.
Maar … de aandachtige lezer ziet misschien al dat dit niet de puzzel is die je in de webshop kan vinden. De verdere uitwerking had namelijk nog wel wat voeten in de aarde; we vertellen je er volgende week alles over in deel 2!