We beloofden in onze vorige blogpost nog vier puzzels die de volle drie dimensies mooi benutten. Wie onze socials volgt, heeft al enkele hints en prototypes zien passeren, maar we willen ze hier toch nog even kort voorstellen en een klein stukje van het verhaal erachter vertellen.
Laten we beginnen met wat qua praktische uitvoering de eenvoudigste puzzel lijkt. Een van de uitdagingen die we stellen, is het maken van een zo lang mogelijke brug uit houten latjes … maar zonder bevestigingsmaterialen zoals touw, lijm of spijkers te gebruiken! Het principe achter de puzzel gaat terug tot de schetsen van Leonardo da Vinci en nog oudere traditionele Chinese bruggen. Het is best verrassend te merken hoe ver je kan geraken en hoe (relatief) stevig het resultaat is.
Voor een klein huis-tuin-en-keukenexperimentje volstaan enkele friscostokjes uit de knutselwinkel, maar voor een festival is dat toch maar wat kleintjes. Dus begon de zoektocht naar grotere, splintervrije, maar nog steeds betaalbare stokjes (gezien de nodige hoeveelheid). Laten we zeggen dat we na al dit experimenteren even geen roerstokjes meer hoeven te kopen … Niet alleen is de dikte van de latjes best belangrijk voor de globale vorm van de brug, ook de buigbaarheid bleek een heikel punt. Zo bleken harsspatels (die wat op friscostokjes lijken) al bij een brug van een kleine twee meter veel te sterk door te buigen. Uiteindelijk bleken mengstokjes voor verf de meest geschikte puzzelstukken, al waren die niet zo makkelijk te vinden zonder inkepingen, logo’s of andere opschriften. We nemen ook wat kleine friscostokjes mee voor kleine handjes die met de grote verfstokken misschien niet zo goed overweg kunnen.
Uiteindelijk besloten we buiten een echt lange brug te gaan bouwen, omdat die binnen moeilijk op foto te krijgen was. De tuin is echter niet de makkelijkste omgeving om te werken. Tussen oneffen gras en een beetje wind bleek het een leuke uitdaging! Gelukkig hebben we op het festival tafels en een beetje beschutting.
Aan het andere uiteinde van het spectrum bevindt zich onze koolstofknikkerspuzzel. Hier waren verschillende prototypes en wat designwerk voor nodig, maar het materiaal hadden we allemaal al in huis. Deze puzzel werd dan ook de afgelopen weken in verschillende fasen samengesteld.
Het idee kwam er na het zien van een volkspel dat (onder andere) het “kaasspel” zou heten: een eenvoudig concept waarbij je met een knikker een traject moet afleggen op een lichtjes hellende wand met gaten in. Je beweegt de knikker door middel van twee touwtjes vastgemaakt aan een houdertje. Uiteraard is het de bedoeling dat je de knikker rond de gaten navigeert en die er niet door valt.
Daar moest wel een leuke wetenschappelijke inkleding voor te vinden zijn … en na even brainstormen vonden we dat ook, in de chemie. We hoopten een toffe neerslagreactie te kunnen vinden tussen een opborreld gas (de knikker) en een vloeistof, die dan een neerdwarrelend reactieproduct zouden opleveren, maar zonder veel succes eigenlijk. We landden echter op iets gelijkaardigs: CO₂-vangende installaties gebaseerd op een vloeibaar mengsel van opgeloste amines. Dat systeem wordt zowel toegepast om aardgas te verfijnen als om rookgassen minder schadelijk te maken voor het klimaat. We besloten meteen om voor die tweede invulling te gaan: de gaten in het bord stellen dus amines voor die de CO₂-knikkers trachten “vangen”.
Op naar een eerste prototype . Dat leek best haalbaar, maar er waren nog wel wat struikelblokken om weg te werken. Waar het ontwerpen van doosjes en kastjes om te lasersnijden ondertussen vlot gaat, hadden we hier best wat moeite mee. Loodrechte hoeken zijn zoveel makkelijker om mee te werken als je iets ineen wil knutselen! Ondanks het gepruts aan de achterkant was dit mini-prototype stevig genoeg om eens uit te testen. We hadden nog geen hangertje uitgedacht, dus gingen we even in de kasten rommelen voor eender wat lusvormigs … Netjes was het niet, maar het werkte! Een paar dagen later maakten we tal van houdertjes uit hout en acryl om te experimenteren. Voor de structuur zelf ging het gelukkig een stuk sneller, het tweede prototype was al raak.

We konden dus naar hartenlust gaan testen. Wat al snel opviel, is dat je knikker eigenlijk echt niet zo veel bewegingsruimte nodig heeft om de gaten te vermijden. Bij de versie op grote schaal besloten we de gaten dan ook een stuk dichter bij elkaar te zetten, zeker naar het einde van het parcours toe.
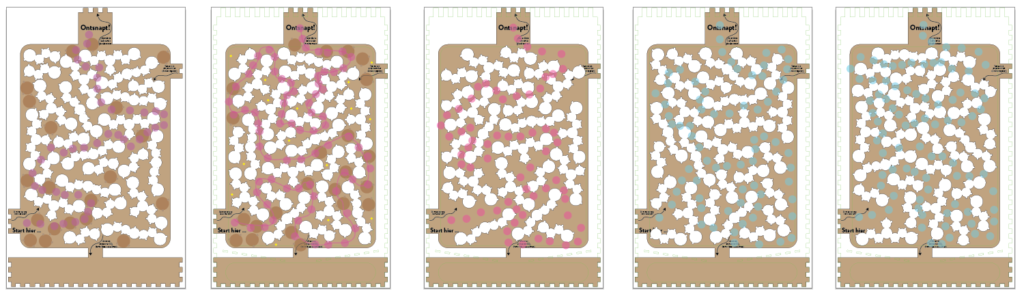
Na verscheidene digitale mock-ups besloten we er ene op volledige grootte te maken. Gelukkig was het geheel zo ontworpen dat de voorplaat makkelijk te vervangen is. Door zijn grootte en het gebruik van 6mm mdf (voor de stevigheid) had de lasercutter wel wat tijd nodig voor deze puzzel.
Met een test op grote schaal waren we overtuigd van de lay-out. Wel hadden we nog heel wat discussies over het toevoegen van bonuspunten, het aanduiden van een verplichte route, … We besloten het uiteindelijk gewoon uit te testen, en wie weet maken we na het festival eens een versie 2.0 mét aangeduid pad op basis van de feedback van puzzelaars. Er was wel consensus dat de watermoleculen nogal stoorden en dat een beetje meer stevigheid nodig was, dus gingen we terug naar de lasercutter. Dit keer ging het een stuk sneller gezien er bijna uitsluitend gesneden moest worden en de rest van de structuur herbruikt kon worden.
De puzzels met zowat de langste tijd tussen idee en uitvoering was een klassieker op een heel andere manier. De torens van Hanoi zijn wellicht bekend genoeg, maar voor de zekerheid: op een bord met drie staven staat een piramide van schijven in verschillende groottes rond één staaf, en het is de bedoeling dat je die hele piramide naar een andere staaf verplaatst krijgt. Je mag telkens maar één schijf verplaatsen en nooit of te nimmer een grotere schijf bovenop een kleinere leggen.
Alle ideëen voor een mooie uitvoering opsommen zou ons véél te ver leiden maar er zijn er heel wat de revue gepasseerd: herbruiken van bestaand kinderspeelgoed, stapelbakjes, verschillende zaagtechnieken voor cirkels, hotwiresnijden van piepschuim … Uiteindelijk besloten we het niet te wagen om hout rond te proberen zagen en opteerden we voor een meteen ook kindvriendelijker materiaal: EVA-foam. Een materiaal dat je misschien kent van de klassieke ineenpuzzelbare speelmatten en dat probleemloos zou moeten lasersnijden.
Inderdaad, EVA-foam bleek heel goed te bewerken met de laser, ook al was het materiaal 20 mm dik. Daar volgt zeker nog wel eens een uitgebreide techniek-blogpost over … Interessant om op te merken was dat er wel een luchtje aan zat, namelijk een uitgesproken barbecuegeur! Bovendien leken de binnenstukjes op (weliswaar zwartgeblakerde) marshmallows en lieten we de schijven na een wasbeurt dan nog eens drogen in een heuse schuimsaté.
Ondanks het grappen en de chaos kwam er uiteindelijk wel een professionele puzzel uit voort. We hadden de schijven graag nog goud geschilderd, als knipoog naar de originele legende van de puzzel met 64 gouden schijven. Echter, EVA-foam en spuitbusverf lijken niet zo goed overeen te komen … dus meer testen zal nodig zijn en daar hadden we nu helaas even geen tijd meer voor.
Tot slot halen we voor deze laatste puzzel inspiratie uit de algebra. Als je de schilderij wil ophangen aan twee spijkers in de muur, dan kan dat op een heel saaie manier, gewoon over de twee spijkers heen. Maar kan het ook op een originele manier, waarbij de spijkers samen het schilderij vasthouden, maar afzonderlijk niet? Om precies te zijn, kun je het schilderij zó aan de muur hangen dat het op de grond valt wanneer je een van de twee spijkers uittrekt? Wat als je met nog meer spijkers werkt, of als je ze een kleurtje geeft? Tal van leuke uitdagingen om je hoofd over te breken!
Hoewel we hier zoals voor de koolstofknikkers een lasergeneden oplossing hadden kunnen uitwerken, besloten we dat niet te doen. Dat zou ons namelijk beperken tot de grootte van het laserbed, wat voor deze puzzel eerder klein zou zijn. We kozen er uiteindelijk voor om een oud schildersezeltje een nieuwe bestemming te geven als “mobiele muur”. Dat wil niet zeggen dat de lasercutter hier niet gebruikt werd, de koppen van de “spijkers” in de muur werden lasergesneden.
De volgende uitdaging bleek een schilderijtje dat makkelijk op te hangen viel, voldoende gewicht had om mooi te vallen én niet meteen zou breken, splinteren, … en daarnaast ook een ophangmiddel dat niet gedoemd is te eindigen in een pluizig, onontknobbelbaar zootje. Dat eerste vonden we in de vorm van PVC-schuim, ook een nieuw materiaal dat we uittestten. Dat tweede kwam toen we even later sleutelhangers aan het maken waren; we merkten op dat een ketting vlot over zichzelf en de spijkers kan glijden als een touw, maar dat je er wel iets in kan vasthaken in plaats van te moeten knobbelen.
We merkten echter al snel dat je voor sommige ingewikkeldere opgaven een heel eind “touw” nodig hebt en dat toch een groot kluwen wordt. Daarom voegden we nog even een klosje toe. Bovendien miste deze puzzel ook wel wat kleur, dus gingen we de twee types spijkers schilderen én een leuk schilderijtje maken.
Als invulling van het schilderij kozen we voor een vallende appel, als knipoog naar het bekende verhaal waarin Isaac Newton door een onfortuinlijk voorval onder een appelboom geïnspireerd werd tot zijn gravitatietheorie. Vele eeuwen later gaf Albert Einstein met zijn relativiteitstheorie een exactere beschrijving van de zwaartekracht. Ook al zijn Einsteins vergelijkingen bijzonder technisch, ze pasten best mooi rond de appel. Fijn genoeg bleek dit PVC-schuim ook nog eens mooi te sublimeren, waardoor we dit vrolijke resultaat konden maken.
En dat zijn ze dan, onze tien puzzels! Wij hebben ze intussen allemaal ingepakt voor morgen en er uitgebreide bundeltjes met achtergrondinformatie voor geschreven, dus wij zullen er zeker zijn. Als jij nog een last-minute uitstapje zoekt: er zijn nog tickets voor dit weekend! En wie er niet bij kan zijn, die zal binnenkort zeker en vast de sfeer kunnen opsnuiven in onze volgende blogs en fotoreeksen.
























