Blog

Zondag 17 september (de laatste dag dat de tentoonstelling Imaginary te bezichtigen was) vond het evenement MathFest plaats op het prachtige domein Beisbroek in Brugge. Het was een erg geslaagde dag, met veel meer bezoekers dan gehoopt die plezier beleefden aan tal van activiteiten. Wij hadden uiteraard onze XL wiskundige puzzels mee, maar daarnaast waren er nog workshops knutselen met wiskunde, een kampioenschap exotische sudoku’s, demonstraties van robots die Rubik’s Cubes oplossen, experimenten bruggen bouwen uit papier, goochelvoorstellingen, workshops wiskundige weefgetouwen, debatten over het wiskundeonderwijs, en voordrachten van onder andere weerman David Dehenau, wiskundige Ann Dooms, kunstenaar Rinus Roelofs, …

Er was ook een winkelhoekje met nieuwe boeken, waar wij heel wat leuke merchandise mochten aan toevoegen. Het befaamde einsteintegeltje was min of meer de mascotte van MathFest, en we maakten voor de gelegenheid dan ook bijhorende koffietassen, muismatten, sleutelhangers en oor­ringen. Natuurlijk hadden we ook heel wat ander materiaal mee uit onze webshop én kun je onze nieuwe creaties daar intussen terugvinden.

Maar de hoofdact van MathFest was toch wel de poging om een wereldrecord aperiodiek betegelen neer te zetten, precies met het einstein­tegeltje. Wij mochten daar de nodige ondersteuning voor bieden en de praktische organisatie uitwerken. Hoe precies, dat doen we hier uit de doeken. En we kunnen alvast vertellen: de recordpoging was een succes! Met nog een halfuurtje op overschot werd een record gevestigd van 6250 einsteintegeltjes. We haalden er het VTM-nieuws mee en ook wetenschapsmagazine Eos (1) schreef een fijne reportage, die je hier kan nalezen.

Betegelen in theorie

Wanneer je gewoon doelloos probeert om de tegeltjes aan elkaar te leggen, geraak je binnen de kortste keren vast te zitten — ondanks veel schijn­bare symmetrieën en patronen is het een verraderlijk lastig puzzelstukje! Samen met de organisatie van MathFest overwogen we meerdere pistes, zoals de beoogde betegeling simpelweg in zijn geheel op grote bladen afdrukken of projecteren op de vloer om te overdekken met tegeltjes. We zijn uiteindelijk van die ideeën afgestapt, want we zagen een uitnodigende, conceptuele manier van werken in het oorspronkelijke artikel (2) van de ontdekkers van de einstein. Om aan te tonen dat hun tegeltje effectief tot in het oneindige blijft betegelen, stippelden ze namelijk een soort hand­leiding uit.

De praktische inzetbaarbaarheid was helaas beperkt: het bewijs instrueert in feite hoe je tegels moet vervangen door grotere clusters tegels die op gelijkaardige manier in elkaar blijven passen. De tegels van die clusters worden dan opnieuw vervangen door diezelfde clusters en dat kan je blijven herhalen om de betegeling zo groot te maken als je maar wil. Vanuit abstract wiskundig standpunt een heel elegant bewijs, maar praktisch gezien valt dat toch dik tegen: we willen de constructie natuurlijk niet non-stop blijven openschuiven, herinvullen en weer aaneenpuzzelen tijdens de record­poging.

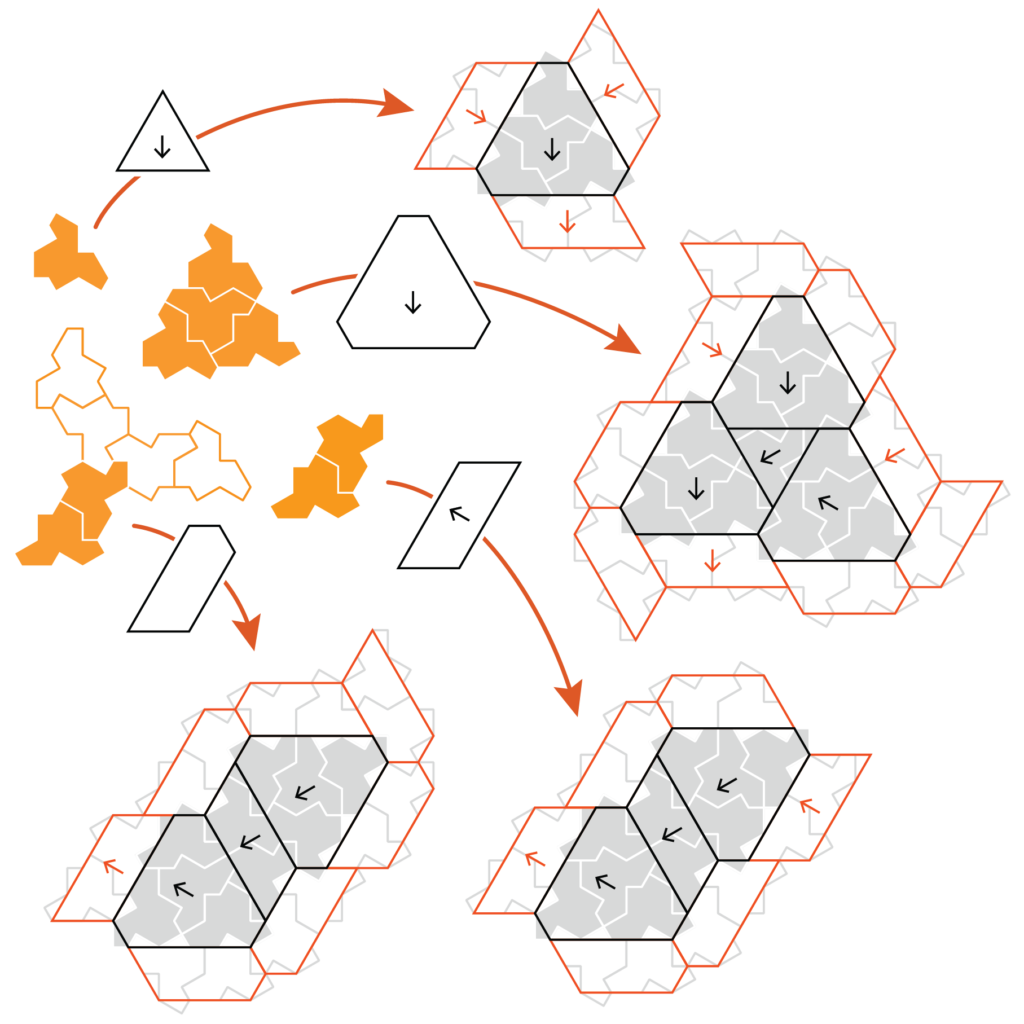
Daarom gingen we omgekeerd te werk: we genereerden op voorhand de betegeling en markeerden daarin die steeds terugkerende clusters, of zoals die gewoonlijk worden genoemd, metategels. Onze hoop was om die afzonderlijk af te drukken op stevige bladen papier, die de bezoekers konden helpen volleggen met losse tegels, om daarna door te spelen naar een centraal team dat alles systematisch aan elkaar puzzelde. Zo zou de record­poging ook nog eens een interactief evenement worden!

De grootste metategel bestaat echter nog steeds uit slechts 13 tegeltjes. Voor de bezoekers geeft zo’n beperkte bijdrage gewoon geen voldoending, en voor het centrale team is de hulpfactor te klein. Daarom keken we een stap verder in de constructie naar de metametategels, de bouwstenen opgebouwd uit metategels. Het was een serieuze evenwichtsoefening: we zochten naar een beperkte set van voorgedrukte patronen die toch vol­doende groot en herkenbaar waren. Uiteindelijk vonden we een bruikbare combinatie van vijf metategels en metametategels, die we voor het gemak gewoon templates noemden.

De organisatie was enthousiast over onze strategie (mede omdat het op die manier ook haalbaar leek om ineens een grootteorde hoger te mikken). Wij werkten dan ook gemotiveerd het template-idee verder uit. Daarnaast ontwierpen we enkele posters om op te hangen bij de recordpoging en het publiek zo een idee te geven wat er juist gebeurt en hoe.

Templates

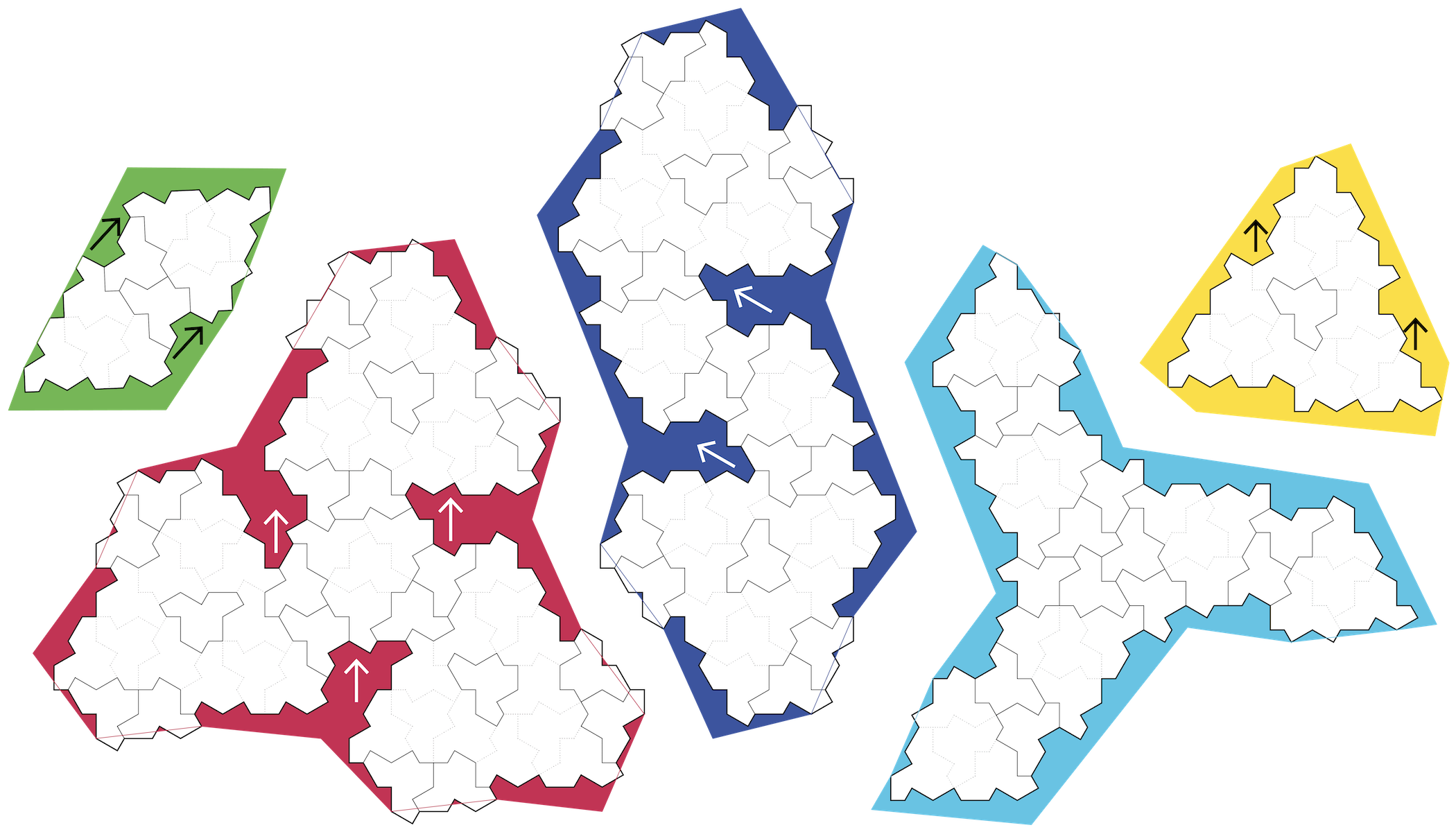
De vijf templates in kwestie staan hieronder afgebeeld. We puzzelden die zo efficiënt mogelijk binnen A3-formaat. De ideale grootte van de tegeltjes bleek zo een slordige 36 op 50 mm en ze werden op die schaal en hoeveelheid uitgesneden door MathFestpartner Ingegno. Wijzelf zorgden voor de templates op stevig papier, voorzien van een kleine rand met een kleurencode. De ochtend van MathFest zelf hielpen enkele vrijwilligers om alle templates — meer dan 160! — uit te knippen.

Op het moment zelf werd alles in goede banen geleid door een vijfkoppig team: vier tussenpersonen die interageerden met het publiek en die de opgevulde templates op hun juiste plek legden, en één bouwmeester die alles overzag. Voor hen drukten we enkele bouwplannen af op groot formaat en met dezelfde kleurencode. Geen overbodige luxe, want het is nog steeds onbegonnen werk om die templates blindelings aan elkaar te proberen leggen.

De aandachtige lezer heeft wellicht enkele vragen!

Wat hebben die pijltjes te betekenen?
Op het eerste (en tweede en derde) zicht lijkt het alsof de templates barsten van symmetrie: de groene en donkerblauwe templates lijken punt­symmetrisch, de rode en gele rotatie­symmetrisch. Dat is helaas maar bedrog. Alleen de licht­blauwe propeller­vormige templates zijn wel degelijk rotatie­symmetrisch; wanneer je de andere templates over 180° of 120° draait, is er een erg subtiel verschil langs de rand — één of twee vlindertjes wijzen naar binnen of juist naar buiten. De figuren hebben dus wel degelijk een oriëntatie, en die is cruciaal om correct te kunnen puzzelen! Dankzij de pijltjes zijn de oriëntaties in één oogopslag af te lezen.

Wat gebeurt er met die grijze tussenruimtes op het bouwplan?
In ons bouwplan gebruiken we een combinatie van metategels van verschillende “ordes”. De grijsgekleurde stukken tussenin zijn paren van einstein­tegels in telkens precies dezelfde vorm. In het abstracte constructiebewijs wordt die opgeblazen naar de vorm die met onze groene template overeen­komt, en die op zijn beurt naar de donkerblauwe template. De reden dat we die niet gewoon mee kunnen nemen in een volwaardig template is nogal technisch … In het originele bewijs horen die zones eigenlijk te overlappen in elke uitbreiding en worden er halve einsteintegels gebruikt om de constructie hard te maken. Er is meestal geen evidente keuze bij welk template een tegel in zo’n overlapzone zou moeten horen — wat werkt op de ene positie, zal ergens anders dubbele tegels opleveren of juist gaten laten.

Daarom besloten we om die overlap in de laagste orde van de constructie niet te mengen met de templates, maar die gewoon achteraf op te vullen met losse tegeltjes. Behalve het extra legwerk waren er eigenlijk alleen maar voordelen! De gekleurde rand van de templates moest bijvoorbeeld niet onder reeds gelegde tegels worden geforceerd en kon dus veel duidelijker en groter (een heleboel knipwerk uitgespaard!). Daarnaast konden we bij de productie de tegels ter opvulling in een ander materiaal laten maken: met lichtergekleurd triplex in plaats van mdf kregen de bouwers een sterke visuele indicatie van het gepuzzel én zag het eindresultaat er nog zovele keren intrigerender uit.

Wat zijn de kleine rode tegeltjes langs de rand van het bouwplan?
Na even rekenen bleek de beoogde betegeling uit precies 6241 einsteintegeltjes te bestaan. Da’s best een mooi getal — 6241 is precies het kwadraat van 79 — maar omwille van de voorziene media-aandacht voor de recordpoging zochten we hoe we op het rondere 6250 konden uitkomen met nog 9 extra tegeltjes.

Betegelen in praktijk

In de namiddag van 17 september werd de aftrap gegeven met de symbolische eerstesteenlegging door Jean Paul Van Bendegem. We hadden op voorhand natuurlijk een vastomlijnde strategie afgesproken met de bouwers, en eenmaal aan de slag verliep alles eigenlijk bijzonder vlot. Niet alleen het centrale team maar vooral ook het publiek was veel gemotiveerder en talrijker dan we hadden durven hopen! Onze vrees dat we zelf een tandje gingen moeten bijsteken met het opvullen van de 160 templates bleek onterecht, want die waren binnen de kortste keren volgelegd. Enkele toe­schouwers zagen een uur later tot hun spijt al geen lege templates meer liggen …

Een anekdote tussendoor. De twee deurwaarders afgevaardigd door International World Records Organisation kwamen uit Nederland. Ze stelden oprecht geïnteresseerde vragen naar de achtergrond en praktische uitvoering van de recordpoging maar kwamen natuurlijk stereotiep streng over. Halverwege werd onze concentratie doorbroken met een gearticuleerd “Nou jongens …” — ik hield mijn hart vast, was er een onregelmatigheid vastgesteld, zagen we ons officiële wereldrecord in rook opgaan? — “… willen jullie een stroopwafel?”

Op de foto’s herken je geen stroopwafels maar wel enkele rode tegels, gesneden uit acryl. De symbolische eerste tegel was een dergelijk opvallend exemplaar. Op het evenement werden die acryl tegels (voornamelijk door jongere kinderen) maar al te graag gemengd onder de bedoelde tegels. Achteraf gezien hadden we die kunnen opnemen in het ontwerp om extra kleur toe te voegen op strategische plekken, maar dat ging het publiek wellicht meer moeite kosten en verwarring opleveren dan het waard was. En het resultaat mag er zeker en vast nog steeds wezen! Na in totaal zo’n drie uur puzzelen, met nog een klein halfuurtje over op de klok, werd de betegeling afgerond.

Daarna was het tijd voor het opmeten en certificeren van de resultaten, voor foto’s en speeches, voor een interview met Jean Paul Van Bendegem voor het VTM-nieuws en met ons voor wetenschapsmagazine Eos (1). Het deed pijn om de betegeling zo snel alweer te moeten afbreken! De laatste aanwezigen konden elk een van de reservetegels meenemen naar huis als aandenken aan deze bijzonder geslaagde eerste editie van MathFest.

Wie weet doen we het volgend jaar over, maar dan met 12 000 tegeltjes? Kun je zo lang niet wachten en wil je zelf aan de slag, of geloof je niet wat er zo lastig is aan puzzelen zonder bouwplan, dan vind je natuurlijk op onze webshop een setje einsteintegels …

1. Eos Wetenschap (20 september 2023), 6250 einsteinhoedjes: wereldrecord aperiodieke betegeling tijdens MathFest Brugge. (↩) (↩)
2. David Smith, Joseph Samuel Myers, Craig Kaplan, Chaim Goodman-Strauss, An aperiodic monotile. ArXiv:2303.10798. (↩)